AC induktor

Betrakta en krets som innehåller en induktor och anta att resistansen i kretsen, inklusive spoltråden, är så liten att den kan försummas. I det här fallet skulle anslutning av spolen till en likströmskälla resultera i en kortslutning, där, som bekant, strömmen i kretsen skulle vara mycket stor.

Situationen är annorlunda när spolen är ansluten till en AC-källa. I detta fall uppstår ingen kortslutning. Detta visar. Vad motstår en induktor mot växelström som passerar genom den.

Vad är kärnan i detta motstånd och hur betingas det?

För att svara på denna fråga, kom ihåg självinduktionsfenomen… Varje förändring av strömmen i spolen gör att en EMF av självinduktion uppstår i den, vilket förhindrar en förändring i strömmen. Värdet av EMF för självinduktion är direkt proportionell mot spolens induktansvärde och förändringshastigheten för strömmen i den. Men eftersom växelström förändras kontinuerligt Den elektromagnetiska strålningen för självinduktion som kontinuerligt uppträder i spolen skapar motstånd mot växelström.

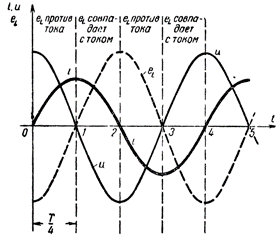
För att förstå de processer som äger rum i växelströmskretsar med induktorn, se grafen.Figur 1 visar krökta linjer som kännetecknar markeringen i kretsen, spänningen i spolen och emk för självinduktion som förekommer i den. Låt oss se till att konstruktionerna i figuren är korrekta.

AC-krets med en induktor

Från ögonblicket t = 0, det vill säga från det första ögonblicket för att observera strömmen, börjar den öka snabbt, men när den närmar sig sitt maximala värde, minskar strömmens ökningshastighet. I det ögonblick då strömmen nådde sitt maximala värde blev hastigheten för dess förändring tillfälligt lika med noll, det vill säga den aktuella förändringen stoppade. Sedan började strömmen till en början långsamt för att sedan snabbt minska och efter periodens andra kvartal sjönk den till noll. Förändringshastigheten för strömmen under denna fjärdedel av perioden, ökande från kulan, når det högsta värdet när strömmen blir lika med noll.

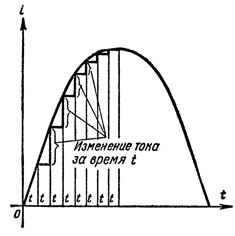
Figur 2. Typen av förändringar i strömmen över tid, beroende på strömmens storlek

Av konstruktionerna i figur 2 kan man se att när strömkurvan passerar genom tidsaxeln så ökar strömmen under en kort tidsperiod T mer än under samma tidsperiod då strömkurvan når sin topp.

Därför minskar strömmens förändringshastighet när strömmen ökar och ökar när strömmen minskar, oavsett strömriktningen i kretsen.

Det är uppenbart att emk för självinduktansen i spolen måste vara störst när strömförändringshastigheten är störst, och minska till noll när dess förändring upphör. I själva verket, på grafen, föll EMF-kurvan för självinduktion eL under det första kvartalet av perioden, med början från det maximala värdet, till noll (se fig. 1).

Under nästa kvartal av perioden minskar strömmen från maxvärdet till noll, men takten för dess förändring ökar gradvis och är störst i det ögonblick då strömmen är lika med noll. Följaktligen ökar EMF för självinduktionen under denna fjärdedel av perioden, som återkommer i spolen, gradvis och visar sig vara ett maximum tills strömmen blir lika med noll.

Riktningen för självinduktions-emk ändrades dock i motsatt riktning, eftersom ökningen av strömmen under periodens första kvartal ersattes under andra kvartalet av dess minskning.

Krets med induktans

Om vi ​​fortsätter med konstruktionen av kurvan för EMF för självinduktion, är vi övertygade om att under perioden för ändring av ström i spolen och EMF för självinduktion i den kommer att slutföra en hel period av dess förändring. Dess riktning är bestämd Lenz lag: med en ökning av strömmen kommer självinduktionens emk att riktas mot strömmen (periodens första och tredje kvartal), och med en minskning av strömmen, tvärtom, sammanfaller den med den i riktning ( andra och fjärde kvartalet av perioden).

Därför förhindrar självinduktionens EMF som orsakas av själva växelströmmen den från att öka, och tvärtom bibehåller den den när den sjunker.

Låt oss nu gå till spolspänningsdiagrammet (se fig. 1). I denna graf visas sinusvågen för spolens terminalspänning lika med och motsatt sinusvågen för självinduktansen emf. Därför är spänningen vid spolens terminaler vid vilket ögonblick som helst lika med och motsatt EMF för självinduktion som uppstår i den. Denna spänning skapas av en generator och går till att dämpa åtgärden i EMF-självinduktionskretsen.

Därför, i en induktor ansluten till en växelströmskrets, skapas motstånd när ström flyter. Men eftersom ett sådant motstånd så småningom inducerar spolens induktans, kallas det induktivt motstånd.

Induktivt motstånd betecknas med XL och mäts, som ett motstånd, i ohm.

Kretsens induktiva resistans är ju större, desto större aktuell källfrekvenskretsförsörjning och större kretsinduktans. Därför är den induktiva resistansen hos en krets direkt proportionell mot strömmens frekvens och kretsens induktans; bestäms av formeln XL = ωL, där ω — cirkulär frekvens bestäms av produkten 2πe... — kretsinduktans i n.

Ohms lag för en växelströmskrets som innehåller ett induktivt motstånd låter Alltså: strömmängden är direkt proportionell mot spänningen och omvänt proportionell mot den induktiva resistansen hos NSi, dvs. I = U / XL, där I och U är de effektiva ström- och spänningsvärdena, och xL är kretsens induktiva resistans.

Med tanke på graferna för förändringen av strömmen i spolen. EMF för självinduktion och spänning vid dess terminaler, vi uppmärksammade det faktum att förändringen i dem vVärden inte sammanfaller i tid. Med andra ord visade sig ström-, spännings- och självinduktions-EMK-sinusoiderna vara tidsförskjutna i förhållande till varandra för den aktuella kretsen. Inom AC-teknik kallas detta fenomen vanligen för fasförskjutning.

Om två variabla kvantiteter ändras enligt samma lag (i vårt fall sinusformade) med samma perioder, samtidigt når sitt maximala värde i både framåt och bakåtriktad riktning och samtidigt minskar till noll, så har sådana variabla storheter samma faser eller, som man säger, matcha i fas.

Som ett exempel visar figur 3 fasanpassade ström- och spänningskurvor. Vi observerar alltid sådan fasmatchning i en AC-krets som endast består av aktivt motstånd.

I det fall där kretsen innehåller induktivt motstånd, ström- och spänningsfaser, som ses i fig. 1 matchar inte, det vill säga det finns en fasförskjutning mellan dessa variabler. Strömkurvan tycks i detta fall ligga efter spänningskurvan med en fjärdedel av perioden.

Därför, när en induktor ingår i en växelströmskrets, sker en fasförskjutning mellan ström och spänning i kretsen, och strömmen släpar efter spänningen i fas med en fjärdedel av perioden... Det betyder att den maximala strömmen inträffar en fjärdedel av perioden efter att den maximala spänningen uppnåtts.

Självinduktionens EMF är i motfas med spolens spänning, släpar efter strömmen med en fjärdedel av perioden. I det här fallet är ändringsperioden för strömmen, spänningen, såväl som EMF för självinduktion förändras inte och förblir lika med förändringsperioden för spänningen hos generatorn som matar kretsen. Den sinusformade karaktären av förändringen i dessa värden bevaras också.

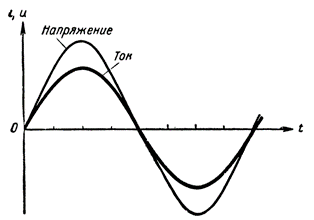
Figur 3. Fasanpassning av ström och spänning i en aktiv motståndskrets

Låt oss nu förstå skillnaden mellan en generatorlast med aktivt motstånd och last med dess induktiva motstånd.

När en växelströmskrets endast innehåller ett aktivt motstånd, absorberas energin från strömkällan i det aktiva motståndet, värma upp tråden.

När kretsen inte innehåller aktivt motstånd (vi betraktar det vanligtvis som noll), utan endast består av spolens induktiva motstånd, spenderas energin från strömkällan inte på att värma upp ledningarna, utan bara på att skapa en EMF av självinduktion , det vill säga det blir magnetfältets energi ... Växelströmmen förändras dock hela tiden både i storlek och riktning, och därför, magnetiskt fält spolen förändras kontinuerligt i takt med att strömmen ändras. Under första kvartalet av perioden, när strömmen ökar, tar kretsen emot energi från strömkällan och lagrar den i spolens magnetfält. Men så snart strömmen, efter att ha nått sitt maximum, börjar minska, bibehålls den på bekostnad av energin som lagras i spolens magnetfält av självinduktionens emk.

Därför får strömkällan, efter att ha gett en del av sin energi till kretsen under periodens första kvartal, den tillbaka från spolen under andra kvartalet, som fungerar som en slags strömkälla. Med andra ord, en växelströmskrets som endast innehåller induktiv resistans förbrukar ingen energi: i detta fall finns det en energifluktuation mellan källan och kretsen. Aktivt motstånd, tvärtom, absorberar all energi som överförs till det från den aktuella källan.

En induktor, till skillnad från en ohmsk resistans, sägs vara inaktiv med avseende på en AC-källa, dvs. reaktiv... Därför kallas spolens induktiva resistans även reaktans.

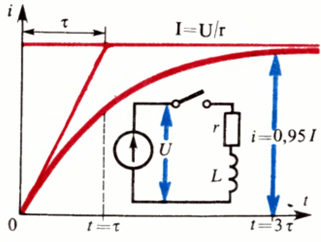
Strömökningskurva vid stängning av en krets som innehåller en induktans — transienter i elektriska kretsar.

Tidigare i denna tråd: El för dummies / Grunderna i elektroteknik

Vad läser andra?

# 1 Postat av: Alexander (4 mars 2010 17:45)

   
är strömmen i fas med generatorns emk? Och dess värde minskar?

#2 skrev: administratör (7 mars 2010 kl. 16.35)

   
I en växelströmskrets som endast består av aktivt motstånd matchar ström- och spänningsfaserna.
       

# 3 skrev: Alexander (10 mars 2010 09:37)

   
Varför är spänningen lika med och motsatt till självinduktionens EMF, trots allt, i det ögonblick då självinduktionens EMF är maximal, är generatorns EMF lika med noll och kan inte skapa denna spänning? Var kommer (spänningen) ifrån?

* I en krets med endast en induktor som inte har något aktivt motstånd, är strömmen som flyter genom kretsen i fas med generatorns emk (emk som beror på rampositionen (i en vanlig generator), inte generatorns spänning)?