Elektromagnetiska vibrationer — utan dämpning och forcerade vibrationer

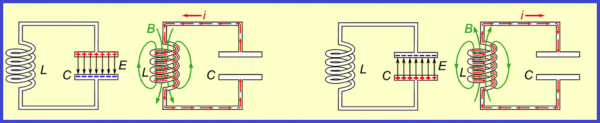
Elektromagnetiska vibrationer i en krets som består av en induktor och en kondensator uppstår på grund av den periodiska omvandlingen av elektrisk energi till magnetisk energi och vice versa. I det här fallet ändras den elektriska laddningen på kondensatorns plattor och storleken på strömmen genom spolen periodiskt.

Elektromagnetiska vibrationer är fria och påtvingade. Fria svängningar dämpas som regel på grund av slingmotstånd som inte är noll, och forcerade svängningar är vanligtvis självsvängningar.

Tillägna sig i en vibrerande krets fria svängningar måste vi först få detta system ur jämvikt: informera kondensatorn med en initial laddning q0 eller på något sätt initiera en strömpuls I0 genom spolen.

Detta kommer att fungera som en slags impuls och fria elektromagnetiska oscillationer kommer att inträffa i kretsen - processen med alternerande laddning och urladdning av kondensatorn genom den induktiva spolen kommer att börja och följaktligen den variabla ökningen och fallet av spolens magnetfält

Oscillationer som upprätthålls i en krets av en extern alternerande elektromotorisk kraft kallas forcerade svängningar. Så, som du redan förstått, är ett exempel på det enklaste oscillerande systemet där fria elektromagnetiska svängningar kan observeras en oscillerande krets som består av en kondensator med elektrisk kapacitet C och en spole med induktans L.

I en riktig oscillerande krets upprepas processen med att ladda kondensatorn periodiskt, men svängningarna dör snabbt ut eftersom energin försvinner huvudsakligen på spoltrådens aktiva motstånd R.

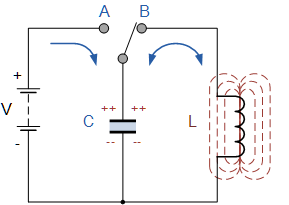
Tänk på en krets med en idealisk oscillerande krets. Låt oss först ladda kondensatorn från batteriet - vi ger den den initiala laddningen q0, det vill säga vi kommer att fylla kondensatorn med energi. Detta kommer att vara den maximala energin för kondensatorn We.

Nästa steg är att koppla bort kondensatorn från batteriet och koppla den parallellt med induktorn. Vid denna tidpunkt kommer kondensatorn att börja ladda ur och en ökande ström kommer att uppstå i spolkretsen. Ju längre kondensatorn laddas ur, desto mer laddning från den passerar gradvis in i spolen, desto större blir strömmen i spolen, således lagrar spolen energi i form av ett magnetfält.

Denna process sker inte momentant utan gradvis, eftersom spolen har induktans, vilket gör att fenomenet självinduktion uppstår, vilket består i att spolen ändå motstår strömökningen. Vid någon tidpunkt når spolens magnetfältsenergi maximalt möjliga värde Wm (beroende på hur mycket laddning som initialt överfördes till kondensatorn och vad kretsens resistans är).

Också, på grund av fenomenet självinduktion, hålls strömmen genom spolen i samma riktning, men dess storlek minskar och den elektriska laddningen ackumuleras så småningom i kondensatorn igen. På så sätt laddas kondensatorn. Dess plattor har nu motsatta laddningstecken än i början av experimentet, när vi kopplade kondensatorn till batteriet.

Kondensatorenergin har nått maximalt möjliga värde för denna krets. Strömmen i kretsen har stannat. Nu börjar processen gå i motsatt riktning, och detta kommer att fortsätta om och om igen, det vill säga att det blir fria elektromagnetiska svängningar.

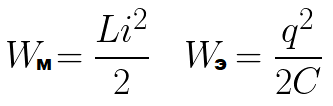
Om det aktiva motståndet för kretsen R är lika med noll, kommer spänningen över kondensatorplattorna och strömmen genom spolen att variera oändligt enligt den harmoniska lagen - cosinus eller sinus. Detta kallas harmonisk vibration. Laddningen på kondensatorplattorna skulle också förändras enligt en harmonisk lag.

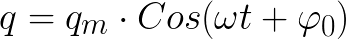
Det finns ingen förlust i den ideala cykeln. Och om det var det, skulle perioden för fria svängningar i kretsen endast bero på värdet på kapacitansen C för kondensatorn och spolens induktans L. Denna period kan hittas (för en ideal slinga med R = 0) med Thomsons formel:

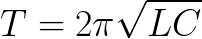
Motsvarande frekvens och cykelfrekvens hittas för en idealisk förlustfri krets med följande formler:

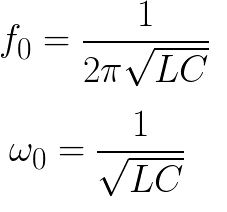
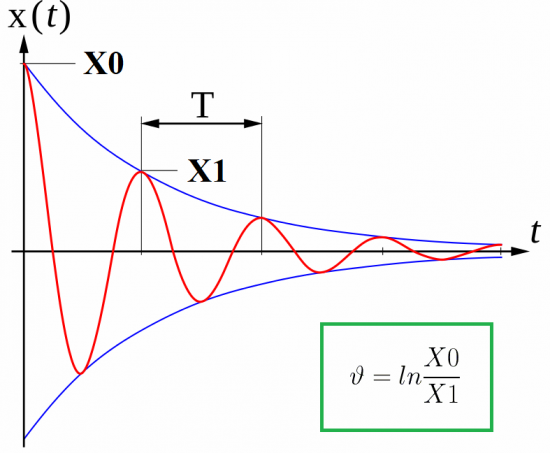
Men idealiska kretsar existerar inte och elektromagnetiska svängningar dämpas på grund av förluster på grund av uppvärmning av ledningarna. Beroende på värdet på kretsresistansen R kommer varje efterföljande maximal kondensatorspänning att vara lägre än den föregående.

I samband med detta fenomen introduceras en sådan parameter som den logaritmiska minskningen av svängningar eller dämpningsdekrement i fysiken. Det finns som den naturliga logaritmen för förhållandet mellan två på varandra följande maxima (av samma tecken) för svängningarna:

Den logaritmiska svängningsreduktionen relateras till den ideala svängningsperioden genom följande samband, där ytterligare en parameter kan införas, den s.k. Dämpningsfaktor:

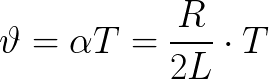
Dämpning påverkar frekvensen av fria vibrationer. Därför skiljer sig formeln för att hitta frekvensen av fria dämpade svängningar i en riktig oscillerande krets från formeln för en ideal krets (dämpningsfaktorn beaktas):

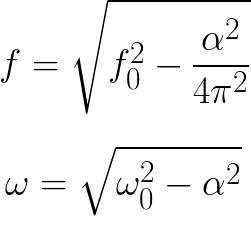
Att göra svängningar i kretsen avstängd, är det nödvändigt att fylla på och kompensera för dessa förluster varje halvperiod. Detta uppnås i kontinuerliga oscillationsgeneratorer, där den externa EMF-källan kompenserar värmeförlusterna med sin energi. Ett sådant svängningssystem med en extern EMF-källa kallas självoscillerande.