Resonans av strömmar

Parallellkoppling av en kondensator och en induktor i en växelströmskrets

Tänk på fenomenen i kedjan växelströmsom innehåller en generator, kondensator och induktor kopplade parallellt. Antag att kretsen inte har något aktivt motstånd.

Uppenbarligen är i en sådan krets spänningen för både spolen och kondensatorn vid varje tidpunkt lika med spänningen som utvecklas av generatorn.

Den totala strömmen i en krets består av strömmarna i dess grenar. Strömmen i den induktiva grenen släpar efter spänningen i fas med en fjärdedel av perioden, och strömmen i den kapacitiva grenen leder den med samma fjärdedel av perioden. Därför visar sig strömmarna i grenarna vid vilket ögonblick som helst vara fasförskjutna i förhållande till varandra med en halv period, det vill säga de är i motfas. Således är strömmarna i grenarna när som helst riktade mot varandra, och den totala strömmen i den oförgrenade delen av kretsen är lika med deras skillnad.

Detta ger oss rätt att skriva likhet I = IL -integralkrets

där jag- effektiva värdet av den totala strömmen i kretsen, I L och integrerad krets — effektiva värden på strömmar i grenarna.

Genom att använda Ohms lag för att bestämma de effektiva värdena för strömmen i grenarna får vi:

Il = U/XL och Az°C = U/XC

Om kretsen domineras av induktivt motstånd, dvs. XL Mer ▼ XC, strömmen i spolen är mindre än strömmen i kondensatorn; därför är strömmen i den oförgrenade delen av kretsen kapacitiv till sin natur och kretsen som helhet för generatorn kommer att vara kapacitiv. Omvänt, med XC större än XL, är strömmen i kondensatorn mindre än strömmen i spolen; därför är strömmen i den oförgrenade delen av kretsen induktiv, och kretsen som helhet för generatorn kommer att vara induktiv.

Man bör inte glömma att i båda fallen är lasten reaktiv, d.v.s. kretsen förbrukar inte generatorns kraft.

Resonans av strömmar

Låt oss nu överväga fallet när kondensatorn och spolen kopplade parallellt visade sig vara lika i sin reaktans, dvs. XlL = X°C.

Om vi, som tidigare, antar att spolen och kondensatorn inte har något aktivt motstånd, då om deras reaktioner är lika (YL = Y° C) kommer den totala strömmen i den oförgrenade delen av kretsen att vara noll, medan i grenarna lika strömmar kommer att flyta med största omfattning. I detta fall uppstår fenomenet resonansströmmar i kretsen.

Vid strömresonans kommer de effektiva värdena för strömmarna i varje gren, bestämda av förhållandena IL = U / XL och Аz° С = U / XC, att vara lika med varandra, så att XL = XC.

Slutsatsen vi kom fram till kan vid första anblicken tyckas ganska märklig. Faktum är att generatorn är belastad med två resistanser och det finns ingen ström i den oförgrenade delen av kretsen, medan lika och dessutom de största strömmarna flyter i själva resistanserna.

Detta förklaras av beteendet hos spolens magnetfält och elektriskt fält hos en kondensator… Vid resonans av strömmar, som i spänningsresonans, det finns en energifluktuation mellan spolens fält och kondensatorns fält. Generatorn, efter att ha kommunicerat energin till kretsen, verkar vara isolerad. Den kan stängas av helt och strömmen i den förgrenade delen av kretsen kommer att bibehållas utan generator av den energi som kretsen initialt lagrar. Dessutom kommer spänningen över kretsterminalerna att förbli exakt densamma som den som utvecklas av generatorn.

När induktorn och kondensatorn är parallellkopplade, fick vi alltså en oscillatorkrets som skiljer sig från den ovan beskrivna endast genom att generatorn som skapar svängningarna inte är direkt ansluten till kretsen och kretsen är sluten. 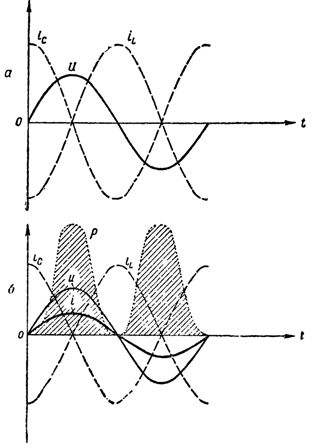Grafer över strömmar, spänning och effekt i kretsen vid resonans av strömmar: a — det aktiva motståndet är lika med noll, kretsen förbrukar inte energi; b — kretsen har ett aktivt motstånd, en ström har uppstått i den oförgrenade delen av kretsen, kretsen förbrukar energi

L, C och e, vid vilka strömresonans uppstår, bestäms, som i spänningsresonans (om vi försummar kretsens aktiva resistans), av likheten:

ωL = 1 / ω°C

Därför:

eres = 1 / 2π√LC

Lres = 1 / ω2C

Styck = 1 / ω2L

Genom att ändra någon av dessa tre kvantiteter kan likheten Xl = X°C uppnås, d.v.s. förvandla kretsen till en oscillerande krets.

Så vi har en sluten oscillerande krets där vi kan inducera elektriska svängningar, d.v.s. växelström. Och om det inte vore för det aktiva motståndet som varje oscillerande krets besitter, skulle en växelström kontinuerligt kunna existera i den.Närvaron av aktivt motstånd leder till det faktum att svängningarna i kretsen gradvis dör ner, och för att upprätthålla dem behövs en energikälla - en generator.

I icke-sinusformade strömkretsar är resonanslägen möjliga för olika övertonskomponenter.

Resonansströmmar används ofta i praktiken. Fenomenet strömresonans används i bandpassfilter som en elektrisk "klämma" som fördröjer en viss frekvens. Eftersom det finns ett betydande strömmotstånd vid frekvensen f kommer spänningsfallet i kretsen vid frekvensen f att vara maximalt. Denna egenskap hos slingan kallas selektivitet, den används i radiomottagare för att isolera signalen från en viss radiostation. En oscillerande krets som arbetar i ett resonansläge av strömmar är en av huvudkomponenterna elektroniska generatorer.