Aktivt motstånd och induktor i AC-krets

Med tanke på en växelströmskrets som endast innehåller induktivt motstånd (se artikeln "Induktor i en växelströmskrets"), antog vi att det aktiva motståndet för denna krets är noll.

Faktum är att både spolens tråd och anslutningstrådarna har ett litet men aktivt motstånd, så kretsen förbrukar oundvikligen energin från strömkällan.

Därför, när man bestämmer det totala motståndet för en extern krets, är det nödvändigt att lägga till dess reaktiva och aktiva motstånd. Men det är omöjligt att lägga till dessa två motstånd som är olika till sin natur.

I detta fall hittas kretsens impedans till växelströmmen genom geometrisk addition.

En rätvinklig triangel (se figur 1) är konstruerad, vars ena sida är värdet på det induktiva motståndet och den andra sidan är värdet på det aktiva motståndet. Den önskade kretsimpedansen bestäms av den tredje sidan av triangeln.

Figur 1. Bestämning av impedansen för en krets som innehåller induktivt och aktivt motstånd

Kretsimpedansen betecknas med den latinska bokstaven Z och mäts i ohm. Av konstruktionen framgår att det totala resistansen alltid är större än det induktiva och aktiva resistansen var för sig.

Det algebraiska uttrycket för den totala kretsresistansen är:

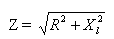
där Z - totalt motstånd, R - aktivt motstånd, XL - kretsens induktiva resistans.

Därför är den totala resistansen hos en krets mot växelström, bestående av aktiv och induktiv resistans, lika med kvadratroten av summan av kvadraterna av den aktiva och induktiva resistansen i denna krets.

Ohms lag eftersom en sådan krets uttrycks med formeln I = U / Z, där Z är kretsens totala resistans.

Låt oss nu analysera vad spänningen blir om kretsen, förutom och och fasförskjutningen mellan strömmen och induktansen, också har ett relativt stort aktivt motstånd. I praktiken kan en sådan krets till exempel vara en krets som innehåller en induktor med järnkärna lindad av en tunn tråd (högfrekvent choke).

I det här fallet kommer fasförskjutningen mellan ström och spänning inte längre att vara en fjärdedel av en period (som det var i en krets med endast induktiv resistans), utan mycket mindre; och ju större resistans, desto mindre fasförskjutning blir resultatet.

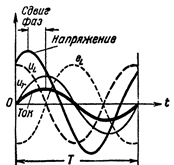
Figur 2. Ström och spänning i en krets som innehåller R och L.

Nu är hon själv EMF för självinduktion är inte i motfas med strömkällans spänning, eftersom den är förskjuten med avseende på spänningen inte med en halv period, utan med mindre.Dessutom är spänningen som skapas av strömkällan vid spolens terminaler inte lika med emk för självinduktion, utan är större än den med mängden spänningsfall i spoltrådens aktiva motstånd. Med andra ord består spänningen i spolen ändå av två komponenter:

• tiL- den reaktiva komponenten av spänningen, som balanserar effekten av EMF från självinduktion,

• tiR- den aktiva komponenten av spänningen som kommer att övervinna kretsens aktiva motstånd.

Om vi ​​kopplar ett stort aktivt motstånd i serie med spolen kommer fasförskjutningen att minska så mycket att den aktuella sinusvågen nästan kommer ikapp spänningens sinusvåg och skillnaden i faser mellan dem blir knappt märkbar.I detta fall, termens amplitud och kommer att vara större än termens amplitud.

På samma sätt kan du minska fasförskjutningen och till och med minska den helt till noll om du minskar frekvensen på generatorn på något sätt. En minskning av frekvensen kommer att resultera i en minskning av självinduktions-EMK och därför en minskning av fasförskjutningen mellan strömmen och spänningen i kretsen som orsakas av den.

Effekten av en växelströmskrets som innehåller en induktor

Växelströmskretsen som innehåller spolen förbrukar inte energin från strömkällan och att det i kretsen sker en energiutbytesprocess mellan generatorn och kretsen.

Låt oss nu analysera hur det kommer att bli med den ström som förbrukas av ett sådant system.

Effekten som förbrukas i en växelströmskrets är lika med produkten av ström och spänning, men eftersom ström och spänning är variabla storheter, kommer effekten också att vara variabel.I det här fallet kan vi bestämma effektvärdet för varje ögonblick i tiden om vi multiplicerar det aktuella värdet med det spänningsvärde som motsvarar ett givet ögonblick.

För att få effektgrafen måste vi multiplicera värdena för de raka linjesegmenten som definierar strömmen och spänningen vid olika tidpunkter. En sådan konstruktion visas i fig. 3, a. Den streckade vågformen p visar hur effekten förändras i en växelströmskrets som endast innehåller induktivt motstånd.

Följande algebraiska multiplikationsregel användes för att konstruera denna kurva: När ett positivt värde multipliceras med ett negativt värde erhålls ett negativt värde, och när två negativa eller två positiva värden multipliceras erhålls ett positivt värde.

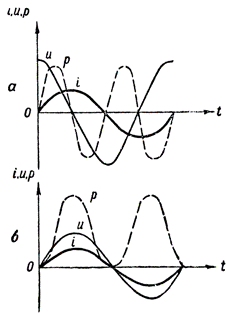
Figur 3. Effektdiagram: a — i en krets som innehåller induktiv resistans, b — även aktiv resistans

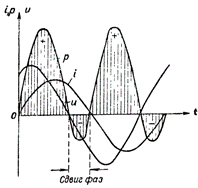
Figur 4. Effektdiagram för en krets som innehåller R och L.

Effektkurvan ligger i detta fall ovanför tidsaxeln. Detta innebär att det inte sker något energiutbyte mellan generatorn och kretsen och därför förbrukas den effekt som generatorn tillför kretsen helt av kretsen.

I fig. 4 visar effektdiagrammet för en krets innehållande både induktivt och aktivt motstånd. I detta fall sker även den omvända överföringen av energi från kretsen till strömkällan, men i mycket mindre utsträckning än i en krets med en enda induktiv resistans.

Efter att ha granskat effektgraferna ovan drar vi slutsatsen att endast fasförskjutningen mellan ström och spänning i kretsen skapar "negativ" effekt.I detta fall, ju större fasförskjutningen är mellan strömmen och spänningen i kretsen, desto mindre effekt kommer kretsen att förbruka, och omvänt, ju mindre fasförskjutningen är, desto större effekt förbrukas av kretsen.

Läs också: Vad är spänningsresonans