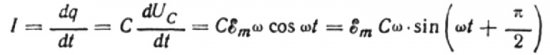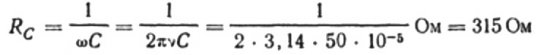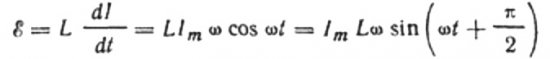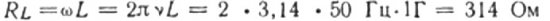Kapacitiv och induktiv resistans i en växelströmskrets

Om vi ​​inkluderar en kondensator i en likströmskrets finner vi att den har oändligt motstånd eftersom en likström helt enkelt inte kan passera genom dielektrikumet mellan plattorna, eftersom ett dielektrikum per definition inte leder en elektrisk likström.

En kondensator bryter DC-kretsen. Men om samma kondensator nu ingår i växelströmskretsen, så visar det sig att dess kondensator inte verkar gå sönder helt, den växlar och laddas helt enkelt, det vill säga den elektriska laddningen rör sig, och strömmen i den externa kretsen är bibehålls.

Baserat på Maxwells teori i detta fall kan vi säga att växelledningsströmmen inuti kondensatorn fortfarande är stängd, bara i detta fall - av förspänningsströmmen. Detta innebär att kondensatorn i AC-kretsen fungerar som en typ av resistans med ändligt värde. Detta motstånd kallas kapacitiv.

Praxis har länge visat att mängden växelström som flyter genom en ledare beror på ledarens form och på de magnetiska egenskaperna hos mediet runt den.Med en rak tråd blir strömmen störst, och om samma tråd lindas till en spole med ett stort antal varv blir strömmen mindre.

Och om en ferromagnetisk kärna införs i samma spole kommer strömmen att minska ännu mer. Därför ger tråden växelström inte bara med ett ohmskt (aktivt) motstånd, utan även med ett extra motstånd, beroende på trådens induktans.Detta motstånd kallas induktiv.

Dess fysiska betydelse är att en föränderlig ström i en ledare med en viss induktans initierar en EMF av självinduktion i den ledaren, som tenderar att förhindra förändringar i strömmen, det vill säga tenderar att minska strömmen. Detta motsvarar att öka trådens motstånd.

Kapacitans i AC-kretsen

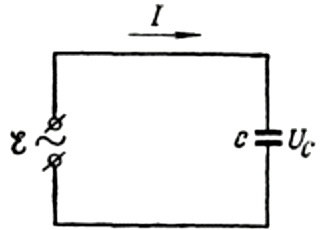
Låt oss först prata om kapacitivt motstånd mer i detalj. Antag att en kondensator med kapacitans C är ansluten till en sinusformad växelströmskälla, då kommer EMF för denna källa att beskrivas med följande formel:

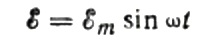
Vi kommer att ignorera spänningsfallet över anslutningsledningarna, eftersom det vanligtvis är mycket litet och kan övervägas separat vid behov. Låt oss nu anta att spänningen över kondensatorplattorna är lika med AC-källans spänning. Sedan:

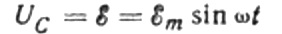
Vid varje givet ögonblick beror laddningen på en kondensator på dess kapacitans och spänningen mellan dess plattor. Sedan, givet den kända källan som nämndes ovan, får vi ett uttryck för att hitta laddningen på kondensatorplattorna genom källspänningen:

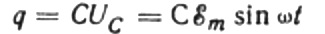
Låt under en oändlig tid dt laddningen på kondensatorn ändras med dq, då kommer en ström I att flyta genom ledningarna från källan till kondensatorn lika med:

Värdet på den aktuella amplituden kommer att vara lika med:

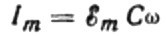
Då blir det slutliga uttrycket för strömmen:

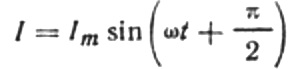
Låt oss skriva om den nuvarande amplitudformeln enligt följande:

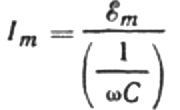
Detta förhållande är Ohms lag, där den reciproka produkten av vinkelfrekvens och kapacitans spelar rollen som motstånd, och är faktiskt ett uttryck för att hitta kapacitansen hos en kondensator i en sinusformad växelströmskrets:

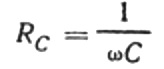
Detta innebär att det kapacitiva motståndet är omvänt proportionell mot strömmens vinkelfrekvens och kondensatorns kapacitans. Det är lätt att förstå den fysiska innebörden av detta beroende.

Ju större kondensatorns kapacitans i AC-kretsen och desto oftare ändras strömriktningen i den kretsen, i slutändan passerar mer total laddning per tidsenhet genom tvärsnittet av ledningarna som ansluter kondensatorn till AC-källan. Detta innebär att strömmen är proportionell mot produkten av kapacitansen och vinkelfrekvensen.

Låt oss till exempel beräkna kapacitansen för en kondensator med en elektrisk kapacitet på 10 mikrofarad för en sinusformad växelströmskrets med en frekvens på 50 Hz:

Om frekvensen var 5000 Hz skulle samma kondensator uppvisa ett motstånd på cirka 3 ohm.

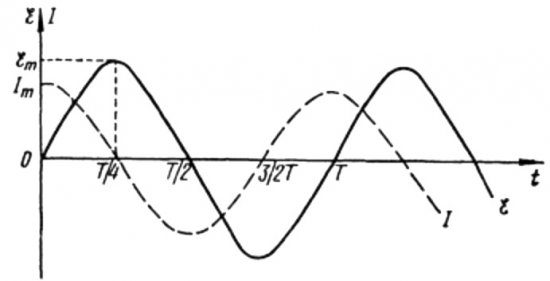
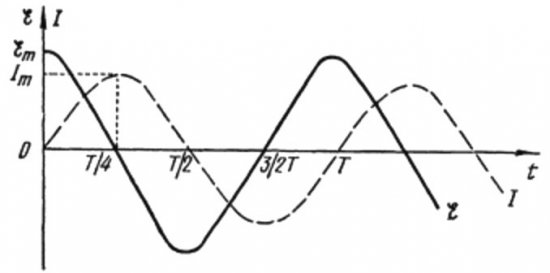
Från formlerna ovan är det tydligt att strömmen och spänningen i en växelströmskrets med en kondensator alltid ändras i olika faser. Strömfasen leder spänningsfasen med pi / 2 (90 grader). Detta innebär att den maximala strömmen i tiden alltid finns en kvartsperiod tidigare än den maximala spänningen. Således leder strömmen över det kapacitiva motståndet spänningen med en fjärdedel av tidsperioden, eller med 90 grader i fas.

Låt oss förklara den fysiska innebörden av detta fenomen.Vid första ögonblicket är kondensatorn helt urladdad, så den minsta spänning som appliceras på den flyttar redan laddningarna på kondensatorns plattor och skapar en ström.

När kondensatorn laddas ökar spänningen över dess plattor, detta förhindrar ytterligare laddningsflöde, så strömmen i kretsen minskar trots ytterligare ökningar i spänningen som appliceras på plattorna.

Detta betyder att om strömmen vid det första ögonblicket var maximal, då när spänningen når sitt maximum efter en kvarts period, kommer strömmen att stanna helt.

I början av perioden är strömmen maximal och spänningen är minimal och börjar öka, men efter en fjärdedel av perioden når spänningen ett maximum, men strömmen har redan sjunkit till noll vid det här laget. Det visar sig alltså att spänningen leder spänningen med en fjärdedel av perioden.

AC induktivt motstånd

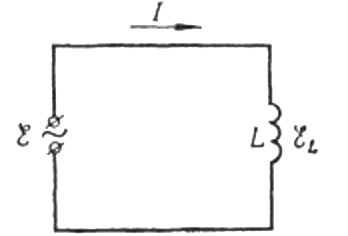
Nu tillbaka till induktivt motstånd. Antag att en sinusformad växelström flyter genom en induktansspole. Det kan uttryckas som:

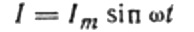
Strömmen beror på växelspänningen på spolen. Detta betyder att en EMF av självinduktion kommer att dyka upp på spolen, vilket uttrycks enligt följande:

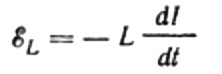
Återigen försummar vi spänningsfallet över ledningarna som ansluter EMF-källan till spolen. Deras ohmska motstånd är mycket lågt.

Låt växelspänningen som appliceras på spolen när som helst balanseras helt av den uppkommande EMF av självinduktion som är lika stor som den i motsatt riktning:

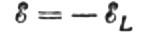
Då har vi rätt att skriva:

Eftersom amplituden för spänningen som appliceras på spolen är:

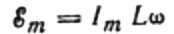
vi får:

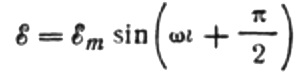
Låt oss uttrycka den maximala strömmen enligt följande:

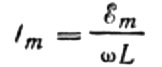
Detta uttryck är i huvudsak Ohms lag. En kvantitet som är lika med produkten av induktansen och vinkelfrekvensen spelar rollen som resistans här och är inget annat än induktorns induktiva resistans:

Så det induktiva motståndet är proportionellt mot spolens induktans och vinkelfrekvensen för växelströmmen genom den spolen.

Detta beror på det faktum att induktiv resistans beror på inverkan av självinduktions-EMK på källspänningen, - självinduktions-EMK tenderar att minska strömmen och ger därför resistans i kretsen. Storleken på självinduktionens emk, som är känt, är proportionell mot spolens induktans och förändringshastigheten för strömmen genom den.

Låt oss till exempel beräkna det induktiva motståndet för en spole med en induktans på 1 H, som ingår i en krets med en strömfrekvens på 50 Hz:

Om kulans frekvens var 5000 Hz, skulle resistansen för samma spole vara ungefär 31 400 ohm. Kom ihåg att spoltrådens ohmska motstånd vanligtvis är några få ohm.

Från formlerna ovan är det uppenbart att förändringarna i strömmen genom spolen och spänningen i den sker i olika faser, och strömmens fas är alltid mindre än spänningens fas vid pi / 2. Därför maximal ström inträffar en kvarts period senare än början av maximal stress.

I induktivt motstånd släpar strömmen efter spänningen med 90 grader på grund av bromseffekten av den självinducerade EMF, vilket förhindrar att strömmen ändras (både ökar och minskar), så den maximala strömmen observeras i kretsen med spolen senare än den maximala spänningen.

Spole och kondensator kombinerad verkan

Om du kopplar en spole med en kondensator i serie med en växelströmskrets, kommer spolspänningen att flytta fram kondensatorspänningen i tid med en halv period, det vill säga med 180 grader i fas.

Kapacitiv och induktiv resistans kallas reaktanter… Energi förbrukas inte i reaktivt motstånd som i aktivt motstånd. Energin som lagras i kondensatorn återförs periodvis tillbaka till källan när det elektriska fältet i kondensatorn försvinner.

Det är samma sak med en spole: eftersom spolens magnetfält skapas av strömmen, ackumuleras energin i den under en fjärdedel av perioden och under nästa fjärdedel av perioden återvänder den till källan. I den här artikeln har vi pratat om sinusformad växelström, för vilken dessa regler följs strikt.

I sinusformade AC-kretsar kallas induktorer med kärnor kvävandeanvänds traditionellt för strömbegränsning. Deras fördel gentemot reostater är att energi inte försvinner i stora mängder som värme.