Beräkning av kondensatorkapacitans

Kapacitans C är kapaciteten hos kondensatorn att acceptera (lagra och hålla) mängden elektricitet Q i ampere-sekunder eller laddningen Q i pendlar. Om du säger till en kropp, till exempel en boll, en elektrisk laddning (mängd elektricitet) Q, så kommer ett elektroskop som är kopplat mellan denna kropp och marken att visa en spänning U (Fig. 1). Denna spänning är proportionell mot laddningen och beror också på kroppens form och storlek.

Förhållandet mellan laddning Q och spänning U uttrycks med formeln Q = C ∙ U.

Proportionalitetskonstanten C kallas kroppens kapacitans. Om kroppen har formen av en kula är kroppens kapacitans proportionell mot kulans r radie.

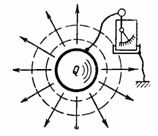
Ris. 1.

Måttenheten för kapacitans är farad (F).

Kroppen har en kapacitans på 1 F när en laddning på 1 k ger en spänning på 1 V. mellan den och marken. Farads är en mycket stor måttenhet, så mindre enheter används i praktiken: microfarad (μF), nanofarad (nF) och picofarad (pF)...

Dessa enheter är relaterade till följande förhållanden: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

Kapacitansen för en boll med en radie på 1 cm är 1,1 pF.

Inte bara en isolerad kropp kan ackumulera laddning, utan också en speciell enhet som kallas en kondensator. En kondensator består av två eller flera plattor (plattor) som är åtskilda av en dielektrikum (isolering).

I fig. 2 visar en krets med en likströmskälla ansluten till en kondensator. När den är påslagen bildas en positiv laddning +Q i kondensatorns högra platta och en negativ laddning -Q i den vänstra plattan. Under kondensatorladdning en ström flyter genom kretsen, som stannar efter avslutad laddning; då blir spänningen över kondensatorn lika med e. etc. c. källa U. Laddningen på kondensatorplattan, spänning och kapacitans är relaterad till förhållandet Q = C ∙ U. I detta fall bildas ett elektrostatiskt fält i kondensatorns dielektrikum.

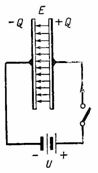
Ris. 2.

Kapaciteten hos en kondensator med ett luftdielektrikum kan beräknas med formeln C = S / (4 ∙ π ∙ d) ∙ 1.11, pF, där S är arean av en platta, cm2; d är avståndet mellan plattorna, cm; C är kondensatorns kapacitans, pF.

Kapaciteten hos en kondensator som består av n plattor (Fig. 3) är lika med: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1.11, pF.

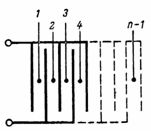
Ris. 3.

Om utrymmet mellan plattorna fylls med ett annat dielektrikum, till exempel papper, kommer kondensatorns kapacitans att öka med en faktor ε. När pappersisolering används kommer kapaciteten att öka 3 gånger, med glimmerisolering - 5-8 gånger, med glas - 7 gånger, etc. Värdet på ε kallas dielektrikumets dielektricitetskonstant.

Den allmänna formeln för att bestämma kapacitansen för en kondensator med dielektrisk konstant ε (epsilon) är: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Denna formel är användbar för att beräkna små variabla kondensatorer för radioapparater.Samma formel kan representeras som: C = (ε_0 ∙ ε ∙ S) / d, där ε_0 är den dielektriska konstanten eller den dielektriska konstanten för vakuumet (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε är dielektrikumets dielektricitetskonstant.

I denna formel ersätts dimensionerna i meter, och kapacitansen erhålls i farad.

Exempel på

1. Vilken kapacitet har planeten Jorden, vars radie är r = 6378 km?

Eftersom kapacitansen för en sfär med en radie på 1 cm är lika med 1,11 pF, är jordens kapacitans: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (Kapaciteten hos en boll av vår planets storlek är relativt liten. Små elektrolytkondensatorer har denna kapacitet).

2. Bestäm kapacitansen för en kondensator som består av två plattor som var och en har en area S = 120 cm2.

Plattorna är åtskilda av ett luftskikt med en tjocklek på d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF ...

3. Bestäm kondensatorns kapacitans med data som ges i föregående exempel, om utrymmet mellan plattorna är fyllt med vaxpapper med en dielektricitetskonstant ε = 4, glas (ε = 7), elektrisk kartong (ε = 2) glimmer (e = 8).

En vaxpapperskondensator har en kapacitans C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Kapacitansen för en glaskondensator är C = 7 ∙ 21,2 = 148,4 pF.

Kapacitansen för kartongkondensatorn är C = 2 ∙ 21,2 = 42,3 pF.

Kapacitansen för glimmerkondensatorn är C = 8 ∙ 21,2 = 169,6 pF.

4. Vad är kapacitansen för en luftroterande kondensator för en radiomottagare bestående av 20 plattor med en area på 20 cm2 om avståndet mellan plattorna är 0,06 cm (bild 149)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Kondensatorn som visas i fig.3, består av separata enklaste kondensatorer med två plattor, vars antal är lika med n-1.

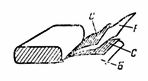
5. En papperskondensator med kapacitans C = 2 μF består av två remsor av stanniol C och två remsor av ett dielektrikum av vaxpapper B med en dielektricitetskonstant ε = 6. Vaxpapprets tjocklek är d = 0,1 mm. De vikta remsorna rullas ihop, ledningarna är gjorda av stålplåtarna. Bestäm längden på kondensorstålbandet om dess bredd är 4 cm (Fig. 4).

Ris. 4.

Först bestämmer vi arean av en remsa med formeln C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, varav S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1.11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Längden på varje remsa är l = 37680/4 = 9420 cm = 94,2 m.