Laddar och laddar ur kondensatorn

Kondensatorladdning

För att ladda kondensatorn måste du ansluta den till DC-kretsen. I fig. 1 visar kondensatorladdningskretsen. Kondensator C är ansluten till generatorns plintar. Nyckeln kan användas för att stänga eller öppna kretsen. Låt oss ta en detaljerad titt på processen att ladda en kondensator.

Generatorn har ett internt motstånd. När omkopplaren är stängd laddas kondensatorn till en spänning mellan plattorna lika med e. etc. v. generator: Uc = E. I detta fall får plattan ansluten till generatorns positiva terminal en positiv laddning (+q), och den andra plattan får en lika negativ laddning (-q). Storleken på laddningen q är direkt proportionell mot kapaciteten hos kondensatorn C och spänningen på dess plattor: q = CUc

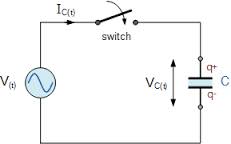
Pe. 1... Kondensatorladdningskrets

För att ladda kondensatorplattorna är det nödvändigt att en av dem vinner och den andra förlorar en viss mängd elektroner.Överföringen av elektroner från en platta till en annan utförs längs den externa kretsen av generatorns elektromotoriska kraft, och processen att flytta laddningar längs kretsen är inget annat än en elektrisk ström, kallad en laddningskapacitiv ström A laddning

Laddningsströmmen i värde flyter vanligtvis i tusendelar av en sekund tills spänningen över kondensatorn når ett värde lika med e. etc. v. generator. Grafen över spänningsökningen på kondensatorns plattor under dess laddning visas i fig. 2, a, av vilken man kan se att spänningen Uc ökar mjukt, först snabbt och sedan allt långsammare, tills den blir lika med e. etc. v. generator E. Därefter förblir spänningen över kondensatorn oförändrad.

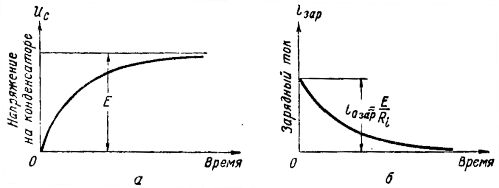
Ris. 2. Grafer över spänning och ström vid laddning av en kondensator

När kondensatorn laddas flyter en laddningsström genom kretsen. Laddningsströmgrafen visas i fig. 2, b. I det initiala ögonblicket har laddningsströmmen det största värdet, eftersom spänningen i kondensatorn fortfarande är noll, och enligt Ohms lag iotax = E /Ri, eftersom alla e., etc. c-generatorn appliceras på motståndet Ri.

När kondensatorn laddas, det vill säga ökar spänningen över den, minskar den för laddningsströmmen. När det redan finns en spänning över kondensatorn blir spänningsfallet över resistansen lika med skillnaden mellan e. etc. v. generator- och kondensatorspänning, dvs lika med E — U s. Därför itax = (E-Us) / Ri

Härifrån kan man se att när Uc ökar, iladdning och vid Uc = E blir laddningsströmmen noll.

Läs mer om Ohms lag här: Ohms lag för en del av en krets

Varaktigheten av kondensatorladdningsprocessen beror på två kvantiteter:

1) från det inre motståndet hos generatorn Ri,

2) från kondensatorns C kapacitans.

I fig. 2 visar graferna för de eleganta strömmarna för en kondensator med en kapacitet på 10 mikrofarad: kurva 1 motsvarar laddningsprocessen från en generator med t.ex. etc. med E = 100 V och med ett internt motstånd Ri= 10 Ohm, motsvarar kurva 2 laddningsprocessen från en generator med samma e. pr. med, men med ett lägre inre motstånd: Ri = 5 ohm.

Från en jämförelse av dessa kurvor kan man se att med ett lägre inre motstånd hos generatorn är styrkan på den eleganta strömmen i det initiala ögonblicket större och därför går laddningsprocessen snabbare.

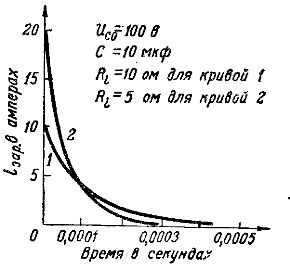
Ris. 2. Grafer över laddningsströmmar vid olika resistanser

I fig. 3 jämför graferna för laddningsströmmar vid laddning från samma generator med t.ex. etc. med E = 100 V och internt motstånd Ri= 10 ohm av två kondensatorer med olika kapacitet: 10 mikrofarad (kurva 1) och 20 mikrofarad (kurva 2).

Initial laddningsström iotax = E /Ri = 100/10 = 10 Båda kondensatorerna är desamma, eftersom en kondensator med större kapacitet lagrar mer elektricitet, då bör dess laddningsström ta längre tid, och laddningsprocessen är mer - lång.

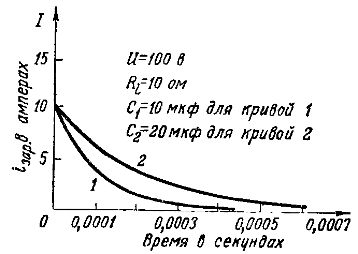
Ris. 3. Tabeller över laddningsströmmar med olika kapacitet

Kondensatorurladdning

Koppla bort den laddade kondensatorn från generatorn och fäst ett motstånd på dess plattor.

Det finns en spänning på plattorna på kondensatorn Us, därför kommer, i en sluten krets, en ström som kallas urladdningskapacitiva ström ires att flyta.

Ström flyter från kondensatorns positiva platta genom motståndet till den negativa plattan. Detta motsvarar övergången av överskottselektroner från den negativa plattan till den positiva, där de saknas.Processen med radramar pågår tills potentialerna för de två plattorna är lika, det vill säga potentialskillnaden mellan dem blir noll: Uc = 0.

I fig. 4a visar grafen för minskningen av spänningen i kondensatorn under urladdning från värdet Uco = 100 V till noll, och spänningen minskar först snabbt och sedan långsammare.

I fig. 4, b visar grafen över förändringarna i urladdningsströmmen. Urladdningsströmmens styrka beror på värdet på motståndet R och enligt Ohms lag ires = Uc/R

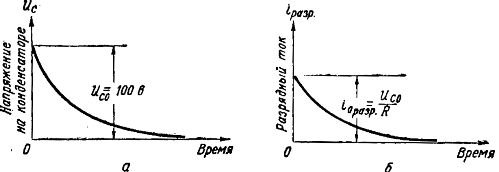
Ris. 4. Grafer över spänning och strömmar under kondensatorurladdning

I det första ögonblicket, när spänningen på kondensatorns plattor är som störst, är urladdningsströmmen också störst, och med en minskning av Uc under urladdningen minskar också urladdningsströmmen. Vid Uc = 0 stannar urladdningsströmmen.

Varaktigheten av bortskaffandet beror på:

1) från kondensatorns C kapacitans

2) på värdet på motståndet R till vilket kondensatorn laddas ur.

Ju större motstånd R är, desto långsammare kommer urladdningen att ske. Detta beror på det faktum att med ett stort motstånd är styrkan på urladdningsströmmen liten och mängden laddning på kondensatorns plattor minskar långsamt.

Detta kan visas i graferna för urladdningsströmmen för samma kondensator, med en kapacitet på 10 μF och laddad till en spänning på 100 V, vid två olika resistansvärden (fig. 5): kurva 1 - vid R =40 ohm, ioresr = UcО/ R = 100/40 = 2,5 A och kurva 2 — vid 20 Ohm ioresr = 100/20 = 5 A.

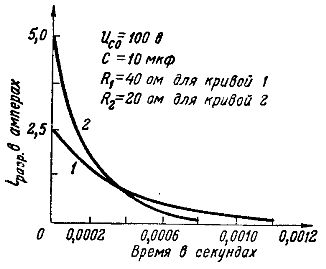
Ris. 5. Grafer över urladdningsströmmarna vid olika resistanser

Urladdningen är också långsammare när kondensatorns kapacitans är stor.Detta beror på att med mer kapacitans på kondensatorplattorna blir det mer elektricitet (mer laddning) och det kommer att ta längre tid för laddningen att tömmas. Detta visas tydligt av graferna för urladdningsströmmarna för två kondensatorer med samma kapacitet, laddade till samma spänning på 100 V och urladdade till ett motstånd R= 40 ohm (Fig. 6: kurva 1 — för en kondensator med en kapacitet på 10 mikrofarad och kurva 2 — för kondensator med en kapacitet på 20 mikrofarad).

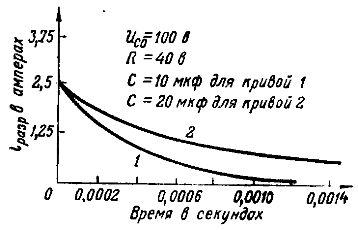
Ris. 6. Grafer över urladdningsströmmarna vid olika styrkor

Från de övervägda processerna kan man dra slutsatsen att i en krets med en kondensator flyter strömmen endast vid laddnings- och urladdningsmomenten, när spänningen på plattorna ändras.

Detta förklaras av det faktum att när spänningen ändras ändras mängden laddning på plattorna, och detta kräver rörelse av laddningar längs kretsen, det vill säga en elektrisk ström måste passera genom kretsen. En laddad kondensator passerar inte likström eftersom dielektrikumet mellan dess plattor öppnar kretsen.

Kondensatorenergi

Under laddningsprocessen lagrar kondensatorn energi genom att ta emot den från generatorn. När en kondensator laddas ur omvandlas all energi i det elektriska fältet till värmeenergi, det vill säga den går till att värma motståndet genom vilket kondensatorn laddas ur. Ju större kondensatorns kapacitans och spänningen över dess plattor är, desto större energi har kondensatorns elektriska fält. Mängden energi som innehas av en kondensator med kapacitet C laddad till en spänning U är lika med: W = Wc = CU2/2

Ett exempel. Kondensator C = 10 μF laddad till spänning Uc = 500 V.Bestäm energin som kommer att frigöras i värmekraften vid det motstånd genom vilket kondensatorn laddas ur.

Svar. Under urladdning kommer all energi som lagras av kondensatorn att omvandlas till värme. Därför W = Wc = CU2/2 = (10 x 10-6 x 500) / 2 = 1,25 J.