Batterier. Räkneexempel

Batterier är elektrokemiska strömkällor som efter urladdning kan laddas med hjälp av elektrisk ström från en laddare. När laddningsströmmen flyter i batteriet uppstår elektrolys, vilket resulterar i att kemiska föreningar bildas på anoden och katoden som fanns på elektroderna i batteriets initiala drifttillstånd.

Elektrisk energi, när den laddas i ett batteri, omvandlas till en kemisk form av energi. När den laddas ur blir den kemiska formen av energi elektrisk. Det tar mer energi att ladda ett batteri än vad som kan erhållas genom att ladda ur det.

Spänningen för varje cell i ett blybatteri efter laddning av 2,7 V bör inte sjunka under 1,83 V vid urladdning.

Medelspänningen för ett nickel-järnbatteri är 1,1 V.

Batteriets laddnings- och urladdningsströmmar är begränsade och inställda av tillverkaren (cirka 1 A per 1 dm2 av plattan).

Mängden elektricitet som kan dras från ett laddat batteri kallas batteriets amperetimmars kapacitet.

Batterier kännetecknas också av energi- och strömeffektivitet.Energiåtergången är lika med förhållandet mellan energin som tas emot under urladdning och energin som går åt för att ladda batteriet: ηen = Araz / Azar.

För ett blybatteri ηen = 70 % och för ett järn-nickelbatteri ηen = 50 %.

Strömutgången är lika med förhållandet mellan mängden el som tas emot under urladdning och mängden el som förbrukas under laddning: ηt = Q gånger / Qchar.

Blybatterier har ηt = 90 % och järn-nickelbatterier ηt = 70 %.

Batteriberäkning

1. Varför är batteriets strömavkastning större än energiåtergången?

ηen = Araz / Azar = (Upp ∙ Ip ∙ tp) / (Uz ∙ Iz ∙ tz) = Upp / Uz ∙ ηt.

Energiåtergången är lika med strömåtergången ηt multiplicerat med förhållandet mellan urladdningsspänningen och laddningsspänningen. Eftersom förhållandet Uр / U3 <1, då ηen <ηt.

2. Ett blybatteri med en spänning på 4 V och en kapacitet på 14 Ah visas i fig. 1. Anslutningen av plattorna visas i fig. 2. Att parallellkoppla plattorna ökar batterikapaciteten. Två uppsättningar plattor är kopplade i serie för att öka spänningen.

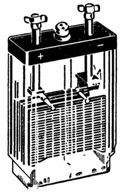
Ris. 1. Blybatteri

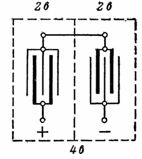
Ris. 2. Anslutning av plattorna på ett blybatteri för en spänning på 4 V

Batteriet laddas på 10 timmar med en ström på Ic = 1,5 A och laddas ur på 20 timmar med en ström på Ip = 0,7 A. Vad är strömeffektiviteten?

Qp = Ip ∙ tp = 0,7 ∙ 20 = 14 A • h; Qz = Iz ∙ tz = 1,5 ∙ 10 = 15 A • h; ηt = Qp / Qz = 14/15 = 0,933 = 93%.

3. Batteriet laddas med en ström på 0,7 A i 5 timmar. Hur länge kommer den att ladda ur med en ström på 0,3 A med en strömutgång ηt = 0,9 (Fig. 3)?

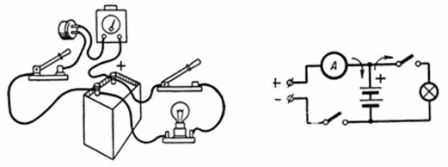
Ris. 3. Bild och diagram till exempel 3

Mängden elektricitet som används för att ladda batteriet är: Qz = Iz ∙ tz = 0,7 ∙ 5 = 3,5 A • h.

Mängden elektricitet Qp som frigörs vid urladdning beräknas med formeln ηt = Qp / Qz, varifrån Qp = ηt ∙ Qz = 0,9 ∙ 3,5 = 3,15 A • h.

Urladdningstid tp = Qp / Ip = 3,15 / 0,3 = 10,5 timmar.

4. 20 Ah-batteriet var fulladdat inom 10 timmar från AC-nätet via en selenlikriktare (Fig. 4). Likriktarens pluspol är ansluten till batteriets pluspol vid laddning. Med vilken ström laddas batteriet om strömverkningsgraden ηt = 90%? Med vilken ström kan batteriet laddas ur inom 20 timmar?

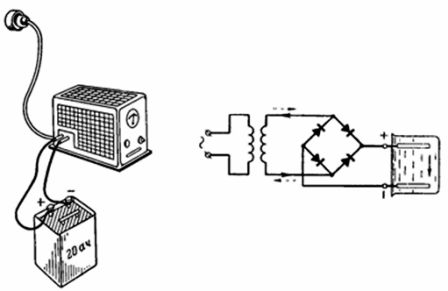
Ris. 4. Bild och diagram till exempel 4

Batteriets laddningsström är: Ic = Q / (ηt ∙ tc) = 20 / (10 ∙ 0,9) = 2,22 A. Tillåten urladdningsström Iр = Q / tr = 20/20 = 1 A.

5. Ett ackumulatorbatteri bestående av 50 celler laddas med en ström på 5 A. en battericell 2,1 V, och dess inre resistans rvn = 0,005 Ohm. Vad är batterispänningen? Vad är etc. c. måste ha en laddningsgenerator med inre resistans rg = 0,1 Ohm (Fig. 5)?

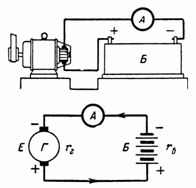
Ris. 5. Bild och diagram till exempel 5

D. d. C. batteri är lika med: Eb ​​= 50 ∙ 2,1 = 105 V.

Batteriets inre resistans rb = 50 ∙ 0,005 = 0,25 Ohm. D. d. S. generator är lika med summan av e. etc. med batterier och spänningsfall i batteri och generator: E = U + I ∙ rb + I ∙ rg = 105 + 5 ∙ 0,25 + 5 ∙ 0,1 = 106,65 V.

6. Batteriet består av 40 celler med internt motstånd rvn = 0,005 Ohm och e. etc. s. 2,1 V. Batteriet laddas med ström I = 5 A från generatorn, t.ex. etc. medvilket är 120 V och det interna motståndet rg = 0,12 Ohm. Bestäm det extra motståndet rd, generatorns effekt, laddningens användbara effekt, effektförlusten i det extra motståndet rd och effektförlusten i batteriet (fig. 6).

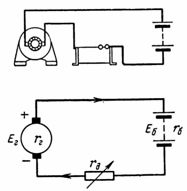
Ris. 6. Beräkning av ackumulatorn

Hitta ytterligare motstånd med hjälp av Kirchhoffs andra lag:

T.ex. = Eb + rd ∙ I + rg ∙ I + 40 ∙ rv ∙ I; rd = (Eg-Eb-I ∙ (rg + 40 ∙ rv)) / I = (120-84-5 ∙ (0,12 + 0,2)) / 5 = 34,4 / 5 = 6,88 Ohm …

Eftersom e. etc. c. När batteriet är laddat är cellens EMF i början av laddningen 1,83V, sedan i början av laddningen, med ett konstant extra motstånd, kommer strömmen att vara mer än 5 A. För att upprätthålla en konstant laddning ström, är det nödvändigt att ändra det extra motståndet.

Effektförlust i det extra motståndet ∆Pd = rd ∙ I ^ 2 = 6,88 ∙ 5 ^ 2 = 6,88 ∙ 25 = 172 W.

Effektförlust i generatorn ∆Pg = rg ∙ I ^ 2 = 0,12 ∙ 25 = 3 W.

Effektförlust i batteriets interna motstånd ∆Pb = 40 ∙ rvn ∙ I ^ 2 = 40 ∙ 0,005 ∙ 25 = 5 W.

Generatorns tillförda effekt till den externa kretsen är Pg = Eb ∙ I + Pd + Pb = 84 ∙ 5 + 172 + 5 = 579 W.

Användbar laddningseffekt Ps = Eb ∙ I = 420 W.