Beräkning av potentiometer och sammansatt shunt

Begrepp och formler

En potentiometer är ett variabelt motstånd med en skjutreglage som ingår som visas i fig.

För mer information se - Potentiometrar och deras tillämpningar

En spänning U appliceras på punkterna 1 och 2. En justerbar spänning tas bort från punkterna 2 och 3, vars värde är mindre än U och beror på skjutreglagets position. Spänningsdelare har ett liknande schema, men de är inte justerbara och har inte ett rörligt skjutreglage.

Potentiometrar, spänningsdelare och komplexa shuntar beräknas med hjälp av Kirchhoffs lagar, såsom beräkning av konventionella kretsar med resistanser.

Exempel på

1. Källspänningen är U = 24 V, potentiometerns totala resistans är r = 300 Ohm. Motorn monteras separat så att r1 = 50 ohm. Vilken spänning U1 kan tas bort från punkterna 3 och 2 (Fig. 1)?

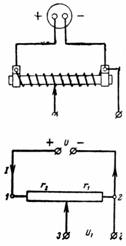
Ris. 1.

Strömmen I och spänningen U över resistansen r är relaterade till formeln I ∙ r = U.

Potentiometerreglaget separerar en del av motståndet, dvs. motståndet r1. Spänningsfallet mellan punkterna 3 och 2 är lika med I ∙ r1 = U1.

Från förhållandet mellan spänningsfallet får vi likheten (I ∙ r1) / (I ∙ r) = U1 / U. Ju större resistans r1, desto större värde på spänningen U1 mellan punkterna 3 och 2 U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. Potentiometern (fig. 2) är laddad på en lampa med resistans r = 100 Ohm. Potentiometern är uppdelad av en reglage i två delar med r1 = 600 Ohm och r2 = 200 Ohm. Bestäm spänningen Ul och lampströmmen Il.

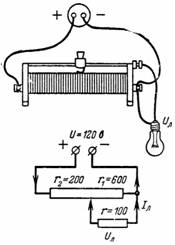
Ris. 2.

Ström I flyter genom resistans r2 och ström Il flyter genom lampan. En ström I-Il flyter genom resistansen r1, vilket skapar en spänning över resistansen r1 lika med lampspänningen: (I-Il) ∙ r1 = Ul.

Å andra sidan är lampspänningen lika med källspänningen minus spänningsfall vid resistans r2: U-I ∙ r2 = Ul.

Strömmen I är lika med källspänningen dividerad med den resulterande resistansen för resistansens serieparallella anslutning:

I = U / (r2 + (r ∙ rl) / (r + rl)).

Vi ersätter uttrycket för källans totala ström i den andra ekvationen:

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.

Efter transformationen får vi ett uttryck för lampspänningen:

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.

Om vi ​​transformerar detta uttryck, utgående från det faktum att Ul = Il ∙ r, får vi ett uttryck för lampströmmen:

Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

Ersätt de numeriska värdena i de resulterande ekvationerna:

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;

Il = Ul/r = 36/100 = 0,36 A.

3. Beräkna spänningen Up och strömmen Ip för mätanordningen som är ansluten till en del av potentiometern. Enheten har ett motstånd på r = 1000 Ohm. Förgreningspunkten delar upp resistansen hos delaren i r2 = 500 ohm och r1 = 7000 ohm (fig. 3).Spänning vid terminalerna på potentiometern U = 220 V.

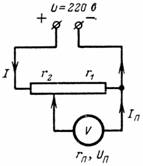
Ris. 3.

Med hjälp av formlerna som erhållits tidigare kan vi skriva att strömmen som flyter genom enheten är:

In = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 500 ∙ 010 00 = 010 400 = 010 000) 1,54 / 11 = 0,14 A.

Upp = Ip ∙ r = 0,14 ∙ 1000 = 14 V.

4. Beräkna enhetens spänning Up, om den förbrukar en ström Ip = 20 mA och är ansluten till en potentiometer uppdelad i resistanserna r2 = 10 ^ 4 Ohm och r1 = 2 ∙ 10 ^ 4 Ohm (Fig. 3).

Den totala spänningen i spänningsdelaren är lika med summan av spänningsfallen i dess delar (genom motstånden r1 och r2): U = I ∙ r2 + I1 ∙ r1; U = I ∙ r2 + Upp

Källströmmen är förgrenad vid motorkontaktpunkten: I = I1 + Ip; I = Upn / r1 + In.

Vi ersätter värdet av strömmen I i spänningsekvationen:

U = (Un / r1 + In) ∙ r2 + Un;

U = Uп / r1 ∙ r2 + Iп ∙ r2 + Uп;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2.

Därför är enhetens spänning Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.

Ersätt de numeriska värdena: Upp = (220-0,02 ∙ 10 000) / 30 000 ∙ 20 000 = 20/3 ∙ 2 = 13,3 V.

5. En likströmskälla med spänning U = 120 V försörjer radiomottagarens anodkretsar genom en potentiometer (spänningsdelare), som tillsammans med filtret har ett motstånd på r = 10000 Ohm. Spänningen U1 tas bort av motståndet r2 = 8000 Ohm. Beräkna anodspänningen vid tomgång och vid lastström I = 0,02 A (fig. 4).

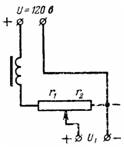
Ris. 4.

Det första fallet liknar exempel 1:

U: U1 = r: r2;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

Det andra fallet liknar exempel 3:

U1 = (U-I ∙ rl) / r ∙ r2;

U1 = (120-0,02 ∙ 2000) / 10000 ∙ 8000 = 64 V.

Vid laddning sjunker spänningen från 96 till 64 V.Om mer spänning behövs, ska skjutreglaget flyttas till vänster, det vill säga motståndet r2 bör ökas.

6. Spänningarna Ua och Ub tas bort av spänningsdelaren. Det totala motståndet för spänningsdelaren ansluten till spänningen U1 = 220 V är r = 20 000 Ohm. Vad är spänningen Ua i motståndet r3 = 12000 Ohm med strömförbrukning Ia = 0,01 A och spänningen Ub i motståndet r2 + r3 = 18000 Ohm med strömförbrukning Ib = 0,02 A (fig. 5).

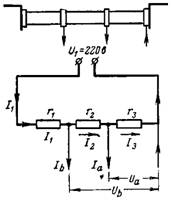
Ris. 5.

Spänningsmotstånd r3

Ua = I3 ∙ r3;

Ua = (U-Ia ∙ (rl + r2) -Ib ∙ rl) / r ∙ r3;

Ua = (220-0,01 ∙ 8000-0,02 ∙ 2000) / 20 000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.

Spänningen Ub är lika med summan av spänningsfallet Ua över motståndet r3 och spänningsfallet över motståndet r2. Spänningsfallet över resistans r2 är lika med I2 ∙ r2. Ström I2 = Ia + I3. Strömmen I3 kan beräknas som i exempel 1:

I3 = (220-80-40) / 20 000 = 0,005 A;

I2 = Ia + I3 = 0,01 + 0,005 = 0,015 A.

Spänning Ub = Ua + I2 ∙ r2 = 5 + 0,015 ∙ 6000 = 150 V.

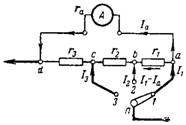
7. Beräkna den kombinerade shunten för milliammetern så att den vid olika lägen av omkopplaren har följande mätområden: I1 = 10 mA; I2 = 30mA; I3 = 100mA. Shuntkopplingsschemat visas i fig. 6. Apparatens inre motstånd ra = 40 Ohm. Inbyggt mätområde på milliammeter 2 mA.

Ris. 6.

Vid mätning av ström I≤2mA stängs shunten av.

a) Vid mätning av strömmen I = 10 mA är omkopplaren i läge 1 och en ström på 10-2 = 8 mA flyter genom alla shuntmotstånd. Spänningsfallet över shuntmotståndet Ush och enheten Ua mellan punkterna d och a måste vara detsamma

Ush = Ua;

(I1-Ia) ∙ (rl + r2 + r3) = Ia ∙ ra;

0,008 ∙ (r1 + r2 + r3) = 0,002 ∙ 40.

b) Vid mätning av ström I2 = 30 mA är omkopplaren i läge 2. Den uppmätta strömmen delas vid punkt b. Vid full avböjning av enhetens pekare kommer strömmen Ia = 2 mA att passera genom motståndet r1 och enheten ra.

Resten av strömmen I2-Ia kommer att passera genom motstånden r2 och r3. Strömmarna kommer att skapa samma spänningsfall över de två grenarna mellan punkterna d och b:

(I2-Ia) ∙ (r2 + r3) = Ia ∙ rl + Ia ∙ ra;

(0,03-0,002) ∙ (r2 + r3) = 0,002 ∙ (r1 + 40).

c) På liknande sätt kommer vi att utföra beräkningen när vi ökar mätområdet till I3 = 100 mA. Ström I3-Ia kommer att flyta genom motstånd r3 och ström Ia genom motstånd r1, r2, ra. Spänningen i båda grenarna är densamma: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;

0,098 ∙ r3 = 0,002 ∙ (r1 + r2 + 40).

Vi fick tre ekvationer med tre okända värden på resistanserna r1, r2 och r3.

Vi multiplicerar alla ekvationer med 1000 och omvandlar dem:

rl + r2 + r3 = 10;

14 ∙ (r2 + r3) -rl = 40;

49 ∙ r3-r1-r2 = 40.

Låt oss lägga till de första och tredje ekvationerna: 50 ∙ r3 = 50;

r3 = 50/50 = 1 ohm.

Låt oss lägga till de första och andra ekvationerna: 15 ∙ r2 + 15 ∙ r3 = 50;

15 ∙ r2 + 15 ∙ 1 = 50;

15 ∙ r2 = 35; r2 = 2,34 ohm.

Låt oss ersätta de erhållna resultaten i den första ekvationen: r1 + 35/15 + 1 = 10;

15 ∙ r1 + 35 + 15 = 150;

r1 = 100/15 = 6,66 ohm.

Korrektheten av beräkningen kan kontrolleras genom att ersätta de erhållna motståndsvärdena i ekvationerna.