Beräkning av det resulterande motståndet i serie-parallellkoppling

Begrepp och formler

En serie-parallell eller blandad anslutning är en komplex koppling av tre eller flera motstånd. Den resulterande resistansen för en blandad anslutning beräknas stegvis med hjälp av formler för beräkning av resistanser i serie- och parallellkopplingar.

Exempel på

1. Beräkna serie-parallellkopplingen av tre resistanser enligt diagrammet i fig. 1.

Byt först ut de parallellkopplade motstånden r2 och r3 med det resulterande motståndet r (2-3):

r (2-3) = (r2 ∙ r3) / (r2 + r3) = (10 ∙ 20) / 30 = 6,6 ohm.

Det resulterande motståndet för hela kretsen är r = r1 + r (2-3) = 5 + 6,6 = 11,6 ohm.

Ris. 1.

2. Vilken ström som flyter genom kretsen (fig. 2) i öppna och slutna fall knivomkopplare P? Hur förändras spänningen över resistans r2 i båda fallen?

Ris. 2.

a) Omkopplaren är öppen. Resulterande resistans för seriekopplade resistanser r1 och r2

r (1-2) = r1 + r2 = 25 ohm.

Ström I (1-2) = U / r (1-2) = 100/25 = 4 A.

Spänningsfall över resistans r2

U2 = I (1-2) ∙ r2 = 4 ∙ 5 = 20 V.

b) Strömbrytaren är stängd. Resulterande resistans hos motstånden r1 och r3 parallellkopplade

r (1-3) = (r1 ∙ r3) / (r1 + r3) = (20 ∙ 10) / (20 + 10) = 200/30 = 6,6 ohm.

Det totala motståndet för hela kretsen är r = r (1-3) + r2 = 6,6 + 5 = 11,6 ohm.

Ström I = U / r = 100 / 11,6 = 8,62 A.

Spänningsfallet över motståndet r2 är i detta fall lika med: U2 = I ∙ r2 = 8,62 ∙ 5 = 43,25 V.

I det andra fallet ökade strömmen som ett resultat av anslutningen av det parallella motståndet R3. Mer aktuellt skapar mer spänningsfall vid motstånd r2.

3. Vad ska vara ytterligare motstånd rd, så att två parallellkopplade lampor för en spänning på 120 V och en ström på 0,2 A kan anslutas till ett nätverk med en spänning på U = 220 V (fig. 3)?

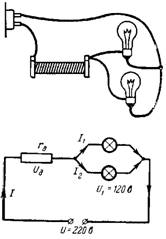
Ris. 3.

Spänningen i lamporna ska vara lika med 120 V. Den återstående spänningen (100 V) faller på det extra motståndet rd. En ström av två lampor I = 0,4 A flyter genom motståndet rd.

Enligt Ohms lag rd = Ud / I = 100 / 0,4 = 250 Ohm.

4. Elektroniska lampor med en 1,2 V-glödtråd och en glödtrådsström på 0,025 och 0,05 A är anslutna i serie till en DC-källa med spänning 4,5 V. Vad bör det extra motståndet rd och parallellt motstånd (shunt) till en lampa med lägre glödtrådsström (fig. 4)?

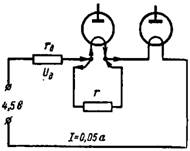
Ris. 4.

Resistanserna i kretsen måste väljas så att den andra lampans glödtrådsström flyter I = 0,05 A. Spänningen över glödtråden hos de elektroniska lamporna kommer att vara 1,2 + 1,2 = 2,4 V. Subtraherar vi detta värde från batterispänningen ta värdet på spänningsfallet över det extra motståndet rd: Ud = 4,5-2,4 = 2,1 V.

Därför är det extra motståndet rd = (Ud) / I = 2,1 / 0,05 = 42 Ohm.

En glödtrådsström på 0,05 A bör inte flöda genom glödtråden i det första vakuumröret. Hälften av denna ström (0,05-0,025 = 0,025 A) måste passera genom shunten r. Shuntspänningen är densamma som lampans glödtråd, d.v.s. 1,2 V. Därför är shuntmotståndet: r = 1,2 / 0,025 = 48 Ohm.

5. Vad är det resulterande kretsmotståndet och strömmen i det i kretsen i fig. 5?

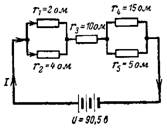
Ris. 5.

Låt oss först bestämma resistansen för de parallellkopplade motstånden:

r (1-2) = (rl ∙ r2) / (rl + r2) = (2 ∙ 4) / (2 + 4) = 8/6 = 1,3 ohm;

r (4-5) = (r4 ∙ r5) / (r4 + r5) = (15 ∙ 5) / (15 + 5) = 75/20 = 3,75 ohm.

Det resulterande kretsmotståndet är:

r = r (1-2) + r3 + r (4-5) = 1,3 + 10 + 3,75 = 15,05 ohm.

Den resulterande strömmen vid spänning U = 90,5 V

I = U / r = 90,5 / 15,05 = 6 A.

6. Beräkna det resulterande motståndet för en komplex serie-parallellkoppling i kretsen i fig. 6. Beräkna den resulterande strömmen I, ström I4 och spänningsfallet över resistans r1.

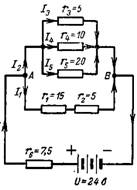
Ris. 6.

Resulterande konduktans av parallellkopplade resistanser

1 / r (3-4-5) = 1 / r3 + 1 / r4 + 1 / r5 = 1/5 + 1/10 + 1/20 = 7/20 sim;

r (3-4-5) = 20/7 = 2,85 ohm.

Kretsresistansen för r1 och r2 är:

r (1-2) = r1 + r2 = 15 + 5 = 20 ohm.

Den resulterande konduktiviteten och resistansen mellan punkterna A och B är lika: 1 / rAB = 1 / r (3-4-5) + 1 / r (1-2) = 7/20 + 1/20 = 8/20 sim ; rAB = 20/8 = 2,5 ohm.

Det resulterande motståndet för hela kretsen är r = rAB + r6 = 2,5 + 7,5 = 10 ohm.

Den resulterande strömmen är I = U / r = 24/10 = 2,4 A.

Spänningen mellan punkterna A och B är lika med källspänningen U minus spänningsfallet över motståndet r6

UAB = U-I ∙ r6 = 24-(2,4 ∙ 7,5) = 6V.

Resistansen r4 är ansluten till denna spänning, så strömmen genom den kommer att vara lika med:

I4 = UAB / r4 = 6/10 = 0,6A.

Motstånd r1 och r2 har ett gemensamt spänningsfall UAB, så strömmen genom r1 är:

I1 = UAB / r (1-2) = 6/20 = 0,3 A.

Spänningsfall över resistans r1

Ur1 = I1 ∙ r1 = 0,3 ∙ 15 = 4,5 V.

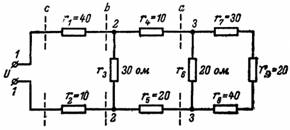
7. Vad är resistansen och strömmen i kretsen i fig. 7 om källspänningen är U = 220 V?

Ris. 7.

Vi börjar med kretsen som ligger till höger om noderna 3 och 3. Resistanserna r7, r8, r9 är seriekopplade, därför

r (7-8-9) = r7 + r8 + r9 = 30 + 40 + 20 = 90 ohm.

Ett motstånd r6 är kopplat parallellt med detta motstånd, så det resulterande motståndet vid nod 3 och 3 (sektion a)

ra = (r6 ∙ r (7-8-9)) / (r6 + r (7-8-9)) = (20 ∙ 90) / (20 + 90) = 1800/110 = 16,36 ohm.

Motstånd r4 och r5 är seriekopplade med motstånd ra:

r (4-5-a) = 10 + 20 + 16,36 = 46,36 ohm.

Resulterande resistans för noderna 2 och 2 (avsnitt b)

rb = (r (4-5-a) ∙ r3) / (r (4-5-a) + r3) = (46,36 ∙ 30) / (46,36 + 30) = 1390,8 / 76, 36 = 18,28 ohm.

Det resulterande motståndet för hela kretsen är r = r1 + rb + r2 = 40 + 18,28 + 10 = 68,28 ohm.

Den resulterande strömmen är I = U / r = 220 / 68,28 = 3,8 A.