Beräkning av shunt för amperemeter

Begrepp och formler

En shunt är ett motstånd som kopplas över amperemeterns terminaler (parallellt med instrumentets interna motstånd) för att öka mätområdet. Den uppmätta strömmen I delas mellan mätshunt (rsh, Ish) och amperemeter (ra, Ia) omvänt proportionella mot deras motstånd.

Shuntmotstånd rsh = ra x Ia / (I-Ia).

För att öka mätområdet med n gånger bör shunten ha ett motstånd rsh = (n-1) / ra

Exempel på

1. Den elektromagnetiska amperemetern har internt motstånd ra = 10 Ohm, och mätområdet är upp till 1 A. Beräkna shuntmotståndet rsh så att amperemetern kan mäta ström upp till 20 A (fig. 1).

Ris. 1.

Den uppmätta strömmen på 20 A kommer att delas upp i en ström Ia = 1 A som kommer att flöda genom amperemetern och en ström Ish som kommer att flöda genom shunten:

I = Ia + Ish.

Därför, strömmen som flyter genom shunten, Ish = I-Ia = 20-1 = 19 A.

Den uppmätta strömmen I = 20 A måste delas i förhållandet Ia: Ish = 1:19.

Det följer att grenmotstånden måste vara omvänt proportionella mot strömmarna: Ia: Ish = 1 / ra: 1 / rsh;

Ia: Ish = rsh: ra;

1:19 = varv: 10.

Shuntmotstånd rsh = 10/19 = 0,526 Ohm.

Shuntmotståndet måste vara 19 gånger mindre än amperemetermotståndet ra så att strömmen Ish passerar genom den, vilket är 19 gånger större än strömmen Ia = 1 A som passerar genom amperemetern.

2. Den magnetoelektriska milliammetern har ett icke-shunt mätområde på 10 mA och ett internt motstånd på 100 Ohm. Vilket motstånd ska shunten ha om enheten ska mäta ström upp till 1 A (Fig. 2)?

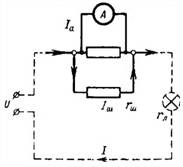
Ris. 2.

Vid full avböjning av nålen kommer strömmen Ia = 0,01 A att passera genom milliammeterns spole och genom shunten Ish:

I = Ia + Ish,

varav Ish = I-Ia = 1-0,99 A = 990 mA.

Strömmen 1 A kommer att delas i omvänd proportion till motstånden: Ia: Ish = rsh: ra.

Från detta förhållande finner vi shuntmotståndet:

10: 990 = rsh: 100; rsh = (10×100) / 990 = 1000/990 = 1,010 Ohm.

Vid full avböjning av pilen kommer ström Ia = 0,01 A att passera genom enheten, ström Ish = 0,99 A genom shunten och ström I = 1 A.

Vid mätning av strömmen I = 0,5 A kommer strömmen Ish = 0,492 A att passera genom shunten och strömmen Ia = 0,05 A passerar genom amperemetern. Pilen avviker till halv skala.

För vilken ström som helst från 0 till 1 A (med den valda shunten) delas strömmarna i grenarna i förhållandet ra: rsh, dvs. 100: 1,01.

3. Amperemetern (Fig. 3) har ett inre motstånd rа = 9,9 Ohm, och resistansen för dess shunt är 0,1 Ohm. Vad är förhållandet mellan den uppmätta strömmen på 300 A i enheten och shunten?

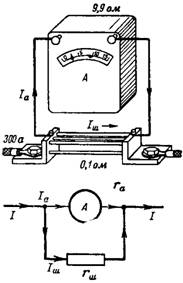
Ris. 3.

Vi kommer att lösa problemet med Kirchhoffs första lag: I = Ia + Ish.

Dessutom Ia: Ish = rsh: ra.

Härifrån

300 = la + Ish;

Ia: Ish = 0,1: 9,9.

Från den andra ekvationen får vi den nuvarande Ia och ersätter den i den första ekvationen:

la = 1/99xIsh;

300 = 1 / 99xIsh + Ish;

Ishx (1 + 1/99) = 300;

Ishx100 / 99 = 300;

Ish = 300 / 100 × 99 = 297 A.

Strömmen i enheten Ia = I-Ish = 300-297 = 3 A.

Från den totala uppmätta strömmen kommer ström Ia = 3 A att passera genom amperemetern och Ish = 297 A genom shunten.

Amperemetershunt

4. En amperemeter vars inre motstånd är 1,98 Ohm ger en full avböjning av pilen vid en ström på 2 A. Det är nödvändigt att mäta strömmen upp till 200 A. Vilket motstånd ska en shunt kopplas parallellt med enhetens terminaler ha?

I denna uppgift ökas mätområdet med en faktor 100: n = 200/2 = 100.

Det erforderliga motståndet för shunten rsh = rа / (n-1).

I vårt fall kommer shuntmotståndet att vara: rsh = 1,98 / (100-1) = 1,98 / 99 = 0,02 Ohm.