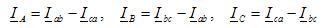Beräkning av trefaskretsar

Kedja trefas växelström består av en trefas strömförsörjning, en trefasförbrukare och kommunikationsledningarna mellan dem.

En symmetrisk trefasförsörjning kan representeras som tre enfasförsörjningar som arbetar på samma frekvens med samma spänning och med en fasvinkel i tiden på 120°. Dessa källor kan vara stjärn- eller deltaanslutna.

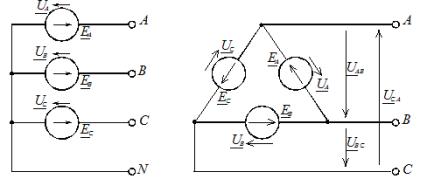
När den är ansluten i en stjärna används den villkorade början av faserna för att ansluta tre linjära ledare A, B, C, och fasernas ändar förenas i en punkt, kallad strömkällans neutrala punkt (trefasgenerator eller transformator). Till denna punkt kan en nollledare N anslutas. Strömkällans stjärnkopplingsschema visas i figur 1, a.

Ris. 1. Anslutningsscheman för strömförsörjningsfaserna: a — stjärna; b — triangel

Spänningen mellan linje och nollledare kallas fas och mellan linjeledare kallas linje (för mer information se här – Linje- och fasspänning).

V integrerad form posterna för uttrycken för fasspänningarna är:

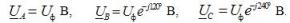
Motsvarande nätspänningar vid stjärnansluten:

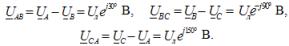
Här är Uf strömkällans fasspänningsmodul och Ul är linjespänningsmodulen. I ett symmetriskt trefassystem, när källfaserna är stjärnkopplade, finns det ett samband mellan dessa spänningar:

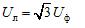
När faserna är kopplade med en triangel, är fasströmförsörjningen seriekopplade i en sluten slinga (Figur 1, b).

Tre linjära ledningar A, B, C förs ut från punkterna för att kombinera källorna med varandra och går till lasten. Från figur 1, b, kan det ses att faskällornas utgångar är anslutna till linjära ledningar, och därför, när faserna hos källan är förbundna med en triangel, är fasspänningarna lika med linjära. I det här fallet finns det ingen neutral tråd.

En last kan anslutas till en trefasförsörjning. Storleks- och naturmässigt kan en trefaslast vara symmetrisk och asymmetrisk.

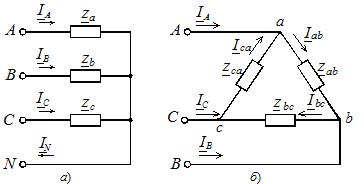
I fallet med en symmetrisk belastning är de komplexa motstånden för de tre faserna desamma, och om dessa motstånd är olika är belastningen obalanserad. Belastningsfaserna kan anslutas till varandra med stjärna eller delta (Figur 2), oavsett källans anslutningsschema.

Ris. 2. Ladda fasanslutningsdiagram

Stjärnanslutningen kan vara med eller utan nollledare (se figur 2, a). Frånvaron av en neutral tråd eliminerar den stela anslutningen av lastspänningen till matningsspänningen, och i fallet med en asymmetrisk fasbelastning är dessa spänningar inte lika med varandra.För att särskilja dem kom vi överens om att använda versaler i bokstavsbeteckningsindexen för matningsspänningarna och strömmarna, och små bokstäver i de belastningsspecifika parametrarna.

Algoritmen för att analysera en trefaskrets beror på belastningsanslutningsschemat, de initiala parametrarna och syftet med beräkningen.

Tvånodsmetoden används för att bestämma fasspänningarna med en obalanserad stjärnkopplad last utan nollledare. Enligt denna metod börjar beräkningen med bestämning av spänningen UN mellan nollpunkterna för matningen och lasten, kallad nollavvikelsespänningen:

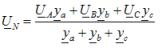
där ya, yb, yc - tillåtna värden för motsvarande belastningsfaser i komplex form

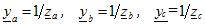
Spänningarna över faserna av en obalanserad last hittas från uttrycken:

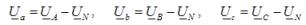
I det speciella fallet med lastobalans, när, i frånvaro av en nollledare, en kortslutning inträffar i en av lastfaserna, är nollförspänningen lika med fasspänningen för matningen av den fas i vilken kortslutningen inträffade.

Spänningen på lastens slutna fas är noll, och på de andra två är den numeriskt lika med linjespänningen. Antag t.ex. att en kortslutning uppstår i fas B. Den neutrala förspänningen för detta fall är UN = UB. Då fasspänningarna på lasten:

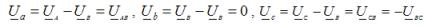
Fasströmmar i lasten, de är också linjeledarströmmar för alla typer av last:

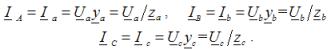
I uppgifterna vid beräkning av trefaskretsar övervägs tre alternativ för att ansluta trefasförbrukare med en stjärna: anslutning till en nollledning i närvaro av konsumenter i tre faser, anslutning till en nollledning i frånvaro av konsumenter i en av faserna, och anslutning utan nollledare med en kort förening i en av belastningsfaserna...

I den första och andra versionen är strömförsörjningens motsvarande fasspänningar placerade på belastningsfaserna och fasströmmarna i belastningen bestäms av formlerna ovan.

I den tredje versionen är spänningen för belastningsfaserna inte lika med fasspänningen för försörjningen och bestäms med hjälp av beroenden

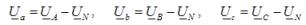
Strömmarna i två okortade faser bestäms enligt Ohms lag, som en bråkdel av divisionen av fasspänningen med impedansen för respektive fas. Kortslutningsströmmen bestäms med hjälp av en ekvation baserad på Kirchhoffs första lagkompilerad för lastens neutrala punkt.

För exemplet ovan på en fas B-kortslutning:

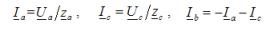
För varje typ av last är den trefasiga aktiva och reaktiva effekten lika med summan av den aktiva respektive reaktiva effekten för de individuella faserna. För att bestämma dessa faseffekter kan du använda uttrycket

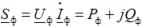
där Uf,Azf, är komplexet av spänningen och komplexet av kopplade strömmar i belastningsfasen; Pf, Qf — aktiv och reaktiv effekt i belastningsfasen.

Trefas aktiv effekt: P = Pa + Pb + Pc

Trefas reaktiv effekt: Q = Qa + Qb + Vc

Trefas skenbar effekt:

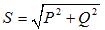
När konsumenterna är anslutna med en triangel, har kretsen den form som visas i figur 2, b. I detta läge är fasanslutningen av den balanserade strömförsörjningen irrelevant.

Spänningar mellan strömförsörjningsledningarna detekteras på belastningsfaserna. Fasströmmarna i lasten bestäms med hjälp av Ohms lag för en del av en kretsAzf = Uf /zf, där Uf — fasspänning i lasten (motsvarande strömkällans nätspänning); zf är det totala motståndet för motsvarande fas av lasten.

Strömmar i linjära ledare bestäms av fasströmmar baserade på Kirchhoffs första lag för varje nod (punkterna a, b, c) i kretsen som visas i figur 2, b: