Ohms lag för en del av en krets
Den grundläggande lag för elektroteknik som du kan använda för att studera och beräkna elektriska kretsar är Ohms lag, som fastställer förhållandet mellan ström, spänning och resistans. Det är nödvändigt att tydligt förstå dess väsen och kunna använda den korrekt för att lösa praktiska problem. Misstag görs ofta inom elektroteknik på grund av oförmågan att korrekt tillämpa Ohms lag.
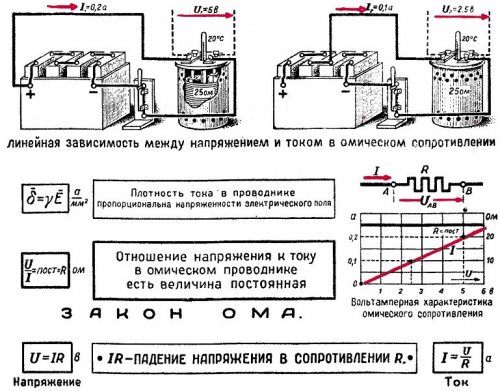
Ohms lag för en del av kretsen säger: strömmen är direkt proportionell mot spänningen och omvänt proportionell mot resistansen.
Om spänningen som verkar i en elektrisk krets ökas flera gånger, kommer strömmen i den kretsen att öka lika mycket. Och om du ökar kretsens motstånd flera gånger, kommer strömmen att minska med samma mängd. På samma sätt är vattenflödet i röret desto större, ju starkare trycket och desto mindre motståndet har röret mot vattnets rörelse.
I en populär form kan denna lag formuleras enligt följande: ju högre spänning för samma motstånd, desto högre ström, och samtidigt, ju högre motstånd för samma spänning, desto lägre är strömstyrkan.
För att uttrycka Ohms lag matematiskt på enklast möjliga sätt, anses motståndet hos en tråd som bär en ström på 1 A vid en spänning på 1 V vara 1 Ohm.
Ström i ampere kan alltid bestämmas genom att dividera spänningen i volt med resistansen i ohm. Därför är Ohms lag för en sektion av en krets skriven i följande formel:
I = U/R.
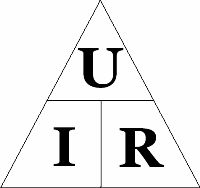
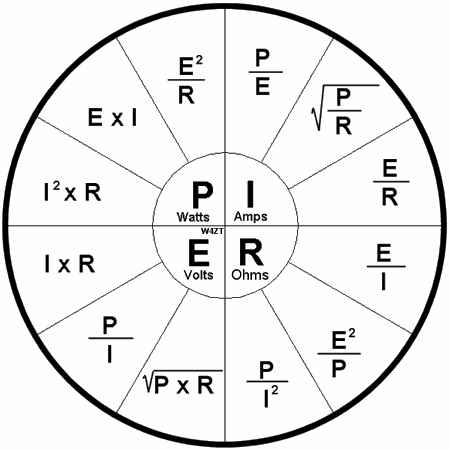
Magisk triangel
Varje sektion eller element i en elektrisk krets kan kännetecknas av tre egenskaper: ström, spänning och motstånd.
Hur man använder Ohms triangel: vi stänger det önskade värdet - två andra symboler ger formeln för dess beräkning. Förresten, bara en formel från triangeln kallas Ohms lag - den som återspeglar strömberoendet av spänning och resistans. De andra två formlerna, även om de är konsekvenser av det, är inte fysiskt vettiga.
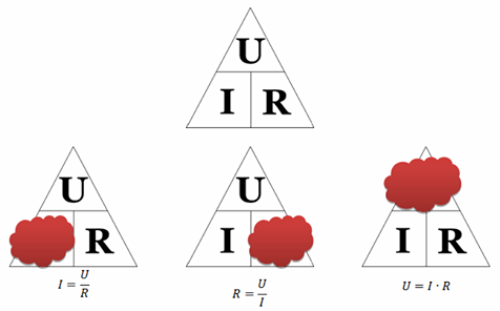
Beräkningar gjorda med Ohms lag för en kretssektion kommer att vara korrekta när spänningen är i volt, resistansen är i ohm och strömmen är i ampere. Om flera enheter av dessa kvantiteter används (t.ex. milliampere, millivolt, megohm, etc.), måste de omvandlas till ampere, volt respektive ohm. För att betona detta skrivs ibland Ohms lagformel för en sektion av en krets på följande sätt:
ampere = volt / ohm
Du kan också beräkna ström i milliampere och mikroampere, medan spänning ska uttryckas i volt och resistans i kilohm respektive megohm.
Andra artiklar om el på ett enkelt och prisvärt sätt:
Vad är spänning, ström och resistans: hur de används i praktiken
Hur motståndet beror på temperaturen
Källor till EMF och ström: huvudsakliga egenskaper och skillnader
Elektriskt och magnetiskt fält – vad är skillnaden?
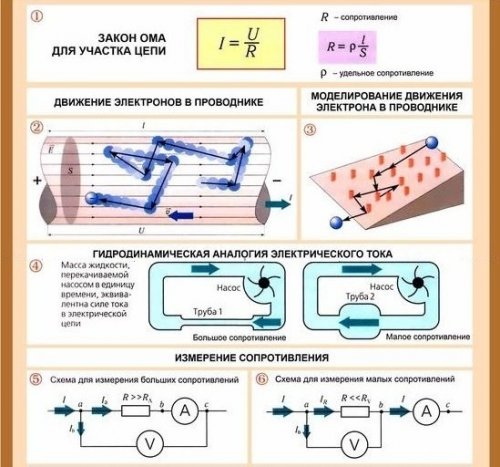
Ohms lag är giltig för varje sektion av kretsen. Om det är nödvändigt att bestämma strömmen i en given sektion av kretsen, är det nödvändigt att dela spänningen som verkar i denna sektion (fig. 1) med motståndet i denna sektion.
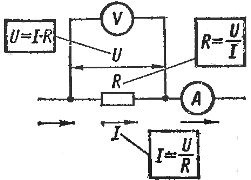
Figur 1. Tillämpning av Ohms lag på en kretssektion
Låt oss ge ett exempel på beräkning av strömmen enligt Ohms lag... Låt det krävas att bestämma strömmen i en lampa med ett motstånd på 2,5 ohm, om spänningen som appliceras på lampan är 5 V. Dividera 5 V med 2,5 ohm, får vi ett värde på ström lika med 2 A. I det andra exemplet bestämmer vi strömmen som kommer att flyta under påverkan av en spänning på 500 V i en krets vars resistans är 0,5 MΩ. För att göra detta uttrycker vi motståndet i ohm. Om vi dividerar 500 V med 500 000 ohm hittar vi strömmen i kretsen, som är 0,001 A eller 1 mA.
När man känner till strömmen och resistansen bestäms ofta spänningen med Ohms lag. Låt oss skriva formeln för att bestämma spänningen
U = IR
Denna formel visar att spänningen i ändarna av en given sektion av kretsen är direkt proportionell mot strömmen och motståndet... Innebörden av detta beroende är inte svårt att förstå.Om resistansen i kretssektionen inte ändras kan strömmen endast ökas genom att öka spänningen. Detta innebär att vid konstant motstånd motsvarar en större ström en högre spänning. Om det är nödvändigt att erhålla samma ström vid olika resistanser, måste det med ett högre motstånd finnas en motsvarande högre spänning.
Spänningen över en sektion av en krets kallas ofta för spänningsfallet... Detta leder ofta till missförstånd. Många tror att spänningsfall är en bortkastad onödig spänning. I verkligheten är begreppen spänning och spänningsfall likvärdiga. Förluster och spänningsfall – vad är skillnaden?
Spänningsfall är det gradvisa fallet i potential över en strömförande krets på grund av att kretsen har ett aktivt motstånd. Enligt Ohms lag är spänningsfallet i varje sektion av kretsen U lika med produkten av resistansen i denna sektion av kretsen R med strömmen i den I, dvs. U — RI. Således, ju större resistans en del av kretsen har, desto större blir spänningsfallet i den delen av kretsen för en given ström.
Beräkningen av Ohms lagspänning kan visas i följande exempel. Låt en ström på 5 mA passera genom en sektion av kretsen med ett motstånd på 10 kOhm, och det är nödvändigt att bestämma spänningen i denna sektion.
Genom att multiplicera A = 0,005 A vid R — 10000 Ω får vi en spänning lika med 50 V. Samma resultat kan erhållas genom att multiplicera 5 mA med 10 kΩ: U = 50 tum
I elektroniska enheter uttrycks ström vanligtvis i milliampere och resistans i kiloohm.Därför är det bekvämt att använda exakt dessa måttenheter i beräkningar enligt Ohms lag.
Ohms lag beräknar också resistans om spänningen och strömmen är kända. Formeln för detta fall är skriven enligt följande: R = U / I.
Motstånd är alltid förhållandet mellan spänning och ström. Om spänningen ökas eller minskas ett antal gånger kommer strömmen att öka eller minska med samma antal gånger. Spännings-strömförhållandet lika med resistansen förblir oförändrat.
Formeln för att bestämma resistans ska inte förstås som att resistansen hos en given ledare beror på ström och spänning. Det är känt att bero på trådens längd, tvärsnittsarea och material. Till utseendet liknar formeln för att bestämma resistans formeln för beräkning av ström, men det finns en grundläggande skillnad mellan dem.
Strömmen i en given sektion av kretsen beror verkligen på spänningen och resistansen och ändras när de ändras. Och motståndet i denna sektion av kretsen är ett konstant värde som inte beror på förändringar i spänning och ström, men är lika med förhållandet mellan dessa värden.
När samma ström flyter i två sektioner av kretsen och de spänningar som tillförs dem är olika, är det tydligt att den sektion till vilken den högre spänningen appliceras har ett motsvarande större motstånd.
Och om, under inverkan av samma spänning, en annan ström flyter i två olika sektioner av kretsen, kommer det i denna sektion alltid att finnas en mindre ström, som har ett större motstånd.Allt detta följer av den grundläggande formuleringen av Ohms lag för en sektion av en krets, det vill säga av det faktum att ju större strömmen är, desto större blir spänningen och desto lägre resistans.
Beräkningen av resistans med hjälp av Ohms lag för en sektion av en krets kommer att visas i följande exempel. Låt det krävas att hitta resistansen för sektionen genom vilken en ström på 50 mA flyter vid en spänning på 40 V. Uttrycka strömmen i ampere får vi I = 0,05 A. Dela 40 med 0,05 och se att motståndet är 800 ohm.
Ohms lag kan visualiseras i form av den så kallade ström-spänningskarakteristiken... Som ni vet är det direkt proportionella förhållandet mellan två storheter en rät linje som går genom origo. Detta beroende brukar kallas linjärt.
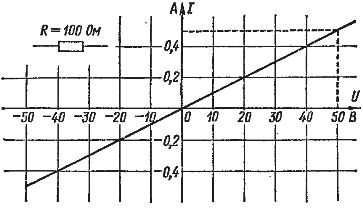
I fig. 2 visas som ett exempel på en graf över Ohms lag för en kretssektion med ett motstånd på 100 ohm. Den horisontella axeln är spänningen i volt och den vertikala axeln är strömmen i ampere. Ström- och spänningsskalan kan väljas efter önskemål. En rät linje dras så att spänning-till-strömförhållandet för var och en av dess punkter är 100 ohm. Till exempel, om U = 50 V, då I = 0,5 A och R = 50: 0,5 = 100 ohm.
Ris. 2... Ohms lag (Karakteristik för strömspänning)
Grafen för Ohms lag för negativa värden på ström och spänning är densamma. Detta innebär att strömmen i kretsen flyter på samma sätt i båda riktningarna. Ju större motstånd, desto mindre ström erhålls vid en given spänning och desto försiktigare rör sig den räta linjen.
Enheter där ström-spänningskarakteristiken är en rät linje som går genom startpunkten, det vill säga motståndet förblir konstant när spänningen eller strömmen ändras, kallas linjära enheter... Termerna linjära kretsar, linjära resistanser används också.
Det finns också enheter där motståndet ändras när spänningen eller strömmen ändras. Då uttrycks förhållandet mellan ström och spänning inte enligt Ohms lag, utan på ett mer komplext sätt. För sådana anordningar kommer ström-spänningskarakteristiken inte att vara en rät linje som går genom startpunkten, utan är antingen en kurva eller en streckad linje. Dessa enheter kallas icke-linjära.
Se även om detta ämne: Tillämpning av Ohms lag i praktiken