Beräkning av värmeelementet

För att bestämma en av huvudparametrarna för värmeelementets tråd - diameter d, m (mm), används två beräkningsmetoder: enligt den tillåtna specifika yteffekten PF och med hjälp av tabellen över nuvarande belastningar.

Tillåten specifik yteffekt PF= P⁄F,

där P är effekten av trådvärmaren, W;

F = π ∙ d ∙ l — värmarens yta, m2; l — trådlängd, m.

Enligt den första metoden

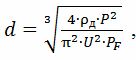
där ρd — elektriskt motstånd hos trådmaterialet vid faktisk temperatur, Ohm • m; U är värmetrådens spänning, V; PF — tillåtna värden för specifik yteffekt för olika värmare:

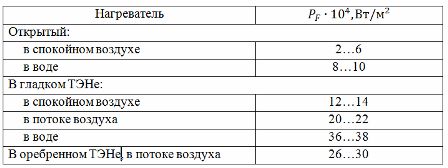
Den andra metoden använder en tabell över aktuella laster (se tabell 1) sammanställd från experimentella data. För att använda den angivna tabellen är det nödvändigt att bestämma den beräknade värmetemperaturen Tp relaterad till den faktiska (eller tillåtna) temperaturen hos ledaren Td med förhållandet:

Tr = Km ∙ Ks ∙ Td,

där Km är installationsfaktorn, med hänsyn till försämringen av värmarens kylförhållanden på grund av dess konstruktion; Kc är den omgivande faktorn, med tanke på förbättringen av värmarens kylförhållanden jämfört med en stationär luftmiljö.

För ett värmeelement tillverkat av tråd tvinnad i en spiral, Km = 0,8 … 0,9; samma, med en keramisk bas Km = 0,6 ... 0,7; för en tråd av värmeplattor och vissa värmeelement Km = 0,5 ... 0,6; för en ledare från ett elektriskt golv, jord och värmeelement Km = 0,3 ... 0,4. Ett mindre värde på Km motsvarar en värmare med mindre diameter, ett större värde till en större diameter.

Vid drift under andra förhållanden än fri konvektion, tas Kc = 1,3 … 2,0 för värmeelement i luftströmmen; för element i stilla vatten Kc = 2,5; i vattenflödet — Kc = 3,0 … 3,5.

Om spänningen Uph och effekten Pf för den framtida (designade) värmaren är inställda, då dess ström (per fas)

Iph = Pph⁄Uph

Enligt det beräknade värdet på värmarens ström för den nödvändiga beräknade temperaturen för dess uppvärmning enligt tabell 1, hittas den erforderliga diametern på nikromtråden d och den erforderliga längden på tråden, m, för tillverkning av värmaren beräknas:

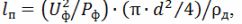
där d är den valda tråddiametern, m; ρd är det specifika elektriska motståndet för ledaren vid den faktiska uppvärmningstemperaturen, Ohm • m,

ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],

där αр — temperaturkoefficient för motstånd, 1/OS.

För att bestämma parametrarna för nikromspiralen, ta medeldiametern för varven D = (6 … 10) ∙ d, spiralens stigning h = (2 … 4) ∙ d,

antal omgångar

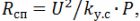
spirallängd lsp = h ∙ n.

Vid beräkning av värmeelementen bör man komma ihåg att motståndet hos spiraltråden efter att ha tryckt på värmeelementet

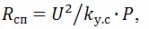
där k (y.s) är en koefficient som tar hänsyn till minskningen av spiralens resistans; enligt experimentella data, k(s) = 1,25. Det bör också beaktas att den specifika yteffekten hos spiraltråden är 3,5 ... 5 gånger större än den specifika yteffekten hos det rörformiga värmeelementet.

I praktiska beräkningar av värmeelementet, bestäm först temperaturen på dess yta Tp = To + P ∙ Rt1,

där det är den omgivande temperaturen, ° C; P är värmeelementets effekt, W; RT1 — termiskt motstånd vid röret — medelgränssnitt, ОC / W.

Därefter bestäms temperaturen på lindningen: Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

där Rt2 är rörväggens termiska motstånd, ОC / W; RT3 — termiskt motstånd för fyllmedlet, ОC / W; Rp1 = 1⁄ (α ∙ F), där α är värmeöverföringskoefficienten, W / (m ^ 2 • ОС); F - värmarens yta, m2; Rt2 = δ⁄ (λ ∙ F), där δ är väggtjockleken, m; λ — väggens värmeledningsförmåga, W / (m • ОС).

För mer information om enheten för värmeelementen, se här: Värmeelement. Anordning, val, drift, anslutning av värmeelement

Tabell 1. Tabell över aktuella laster

Exempel 1. Beräkna elvärmaren i form av en trådspiral enligt den tillåtna specifika yteffekten PF.

Skick.Värmarens effekt P = 3,5 kW; matningsspänning U = 220 V; trådmaterial — nikrom Х20Н80 (en legering av 20 % krom och 80 % nickel), därför den specifika elektriska resistansen hos tråden ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; temperaturkoefficient för motstånd αр = 16 ∙ 10 ^ (- 6) 1 /ОС; spiralen är öppen, i metallisk form, arbetstemperaturen för spiralen är Tsp = 400 ОC, PF= 12 ∙ 10 ^ 4 W / m2. Bestäm d, lp, D, h, n, lp.

Svar. Spolemotstånd: R = U ^ 2⁄P = 220 ^ 2⁄3500 = 13,8 ohm.

Specifik elektrisk resistans vid Tsp = 400 OS

ρ400 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1,11 ∙ 10 ^ (- 6) Ohm • m.

Hitta diametern på tråden:

Från uttrycket R = (ρ ∙ l) ⁄S får vi l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ), därav längden på tråden

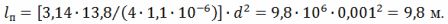
Medeldiametern på spiralvarvet är D = 10 ∙ d = 10 ∙ 0,001 = 0,01 m = 10 mm. Spiraldelning h = 3 ∙ d = 3 ∙ 1 = 3 mm.

Antalet varv i spiralen

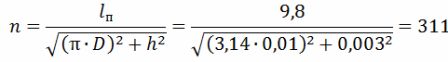
Helixens längd är lsp = h ∙ n = 0,003 ∙ 311 = 0,933 m = 93,3 cm.

Exempel 2. Strukturellt beräkna trådmotståndsvärmaren när du bestämmer tråddiametern d med hjälp av tabellen över strömbelastningar (se tabell 1).

Skick. Trådvärmarens effekt P = 3146 W; matningsspänning U = 220 V; trådmaterial — nikrom Х20Н80 ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; αp = 16 ∙ 10 ^ (- 6) 1 / ℃; öppen spiral placerad i luftströmmen (Km = 0,85, Kc = 2,0); tillåten driftstemperatur för ledaren Td = 470 ОС.

Bestäm diametern d och längden på tråden lp.

Svar.

Tr = Km ∙ Ks ∙ Td = 0,85 ∙ 2 ∙ 470 OS = 800 OS.

Designvärmarens ström I = P⁄U = 3146⁄220 = 14,3 A.

Enligt tabellen över strömbelastningar (se tabell 1) vid Tр = 800 ОС och I = 14,3 A, hittar vi diametern och tvärsnittet av tråden d = 1,0 mm och S = 0,785 mm2.

Trådlängd lp = (R ∙ S) ⁄ρ800,

där R = U ^ 2⁄P = 220 ^ 2⁄3146 = 15,3 Ohm, ρ800 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) ∙11 ] = 1. 10 ^ (- 6) Ohm • m, lp = 15,3 ∙ 0,785 ∙ 10 ^ (- 6) ⁄ (1,11 ∙ 10 ^ (- 6)) = 10,9 m.

Även om nödvändigt, liknande det första exemplet, kan D, h, n, lsp definieras.

Exempel 3. Bestäm den tillåtna spänningen för den rörformade elektriska värmaren (TEN).

Skick... Värmeelementets spiral är gjord av nikromtråd med diameter d = 0,28 mm och längd l = 4,7 m. Värmeelementet är i stillastående luft med en temperatur på 20 °C. Egenskaper för nikrom: ρ20 = 1,1 ∙ 10 ^ (- 6) Ohm • m; αр = 16 ∙ 10 ^ (- 6) 1 / ° C. Längden på den aktiva delen av värmeelementets hölje är La = 40 cm.

Värmeelementet är slätt, ytterdiameter dob = 16 mm. Värmeöverföringskoefficient α = 40 W / (m ^ 2 ∙ ° C). Termiska motstånd: fyllmedel RT3 = 0,3 ОС / W, husväggar Rт2 = 0,002 ОС / W.

Bestäm vilken maximal spänning som kan appliceras på värmeelementet så att dess spoletemperatur Tsp inte överstiger 1000 ℃.

Svar. Värmeelementets temperatur på värmeelementet

Tsp = Till + P ∙ (Rt1 + Rt2 + Rt3),

där det är den omgivande lufttemperaturen; P är värmeelementets effekt, W; RT1 — termisk kontaktmotstånd för rör-medium-gränssnittet.

Värmeelementets effekt P = U ^ 2⁄R,

där R är motståndet för värmeslingan.Därför kan vi skriva Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3), varifrån spänningen på värmeelementet

U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3)).

Hitta R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2),

där ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20)] = (1,12 ∙ — 6) Ohm • m.

Då R = 1,12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4,7) ⁄ (3,14 ∙ (0,28 ∙ 10 ^ (- 3)) ^ 2) = 85,5 Ohm.

Termiskt kontaktmotstånd RT1 = 1⁄ (α ∙ F),

där F är området för den aktiva delen av skalet på värmeelementet; F = π ∙ dob ∙ La = 3,14 ∙ 0,016 ∙ 0,4 = 0,02 m2.

Hitta Rt1 = 1⁄ (40 ∙ 0,02 = 1,25) OC / W.

Bestäm spänningen för värmeelementet U = √ ((85,5 ∙ (1000-20)) / (1,25 + 0,002 + 0,3)) = 232,4 V.

Om den nominella spänningen som anges på värmeelementet är 220 V, kommer överspänningen vid Tsp = 1000 OS att vara 5,6 % ∙ Un.