Enfas växelström

Får växelström

Om tråden A roteras i det magnetiska flödet som bildas av magnetens två poler medurs (fig. 1), då när tråden korsar magnetfältslinjerna, kommer den att inducera e. d. s vars värde bestäms av uttrycket

E = Blvsinα,

där B är den magnetiska induktionen i T, l är längden på tråden i m, v är trådens hastighet i m/s, α — vinkeln med vilken tråden korsar magnetfältslinjerna.

Låt B, I och v för detta fall förbli konstanta, då det inducerade e. etc. c. kommer endast att bero på vinkeln α vid vilken tråden korsar magnetfältet. Så, vid punkt 1, när tråden rör sig längs magnetfältslinjerna, värdet på den inducerade emk. etc. p kommer att vara noll när tråden flyttas till punkt 3 oe. etc. v. kommer att vara av största vikt, eftersom kraftlinjerna kommer att korsas av ledaren i riktningen vinkelrät mot dem, och slutligen t.ex. etc. v. kommer återigen att nå noll om tråden flyttas till punkt 5.

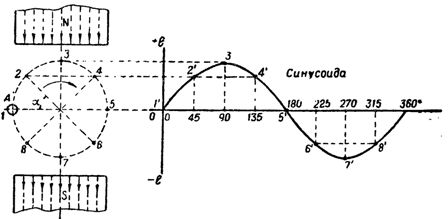
Ris. 1. Ändring av den inducerade e. etc. s. i en tråd som roterar i ett magnetfält

Vid mellanpunkterna 2 och 4, där tråden korsar kraftlinjerna i en vinkel α = 45 °, är värdet på den inducerade emk. etc. c. kommer att vara på motsvarande sätt mindre än vid punkt 3. Sålunda, när tråden vrids från punkt 1 till punkt 5, det vill säga med 180°, kommer det inducerade e. etc. v. ändras från noll till max och tillbaka till noll.

Det är ganska uppenbart att vid en ytterligare rotation av tråd A genom en vinkel på 180° (genom punkterna 6, 7, 8 och 1), arten av förändringen i det inducerade e. etc. p. kommer att vara densamma, men dess riktning kommer att ändras till motsatt, eftersom tråden kommer att korsa magnetfältslinjerna redan under den andra polen, vilket motsvarar att korsa dem i motsatt första riktning.

Därför, när tråden roteras 360°, kommer den inducerade e. etc. v. ändras inte bara i storlek hela tiden, utan ändrar också dess riktning två gånger.

Om tråden är stängd för något motstånd kommer tråden att dyka upp elektricitet, även varierande i storlek och riktning.

Elektrisk ström, som ständigt förändras i storlek och riktning, kallas växelström.

Vad är en sinusvåg?

Ändringens karaktär e. etc. (ström) för ett varv av tråden för större tydlighet, representeras de grafiskt med hjälp av en kurva. Eftersom värdet av e. etc. c. proportionell mot sinα, sedan efter att ha satt vissa vinklar, är det möjligt att med hjälp av tabeller bestämma värdet på sinus för varje vinkel, och på lämplig skala att konstruera en kurva för ändringen av e. etc. c. För att göra detta kommer vi på den horisontella axeln att avsätta trådens rotationsvinklar och på den vertikala axeln, i lämplig skala, det inducerade e. etc. med

Om tidigare indikerat i fig.1 koppla ihop punkterna med en jämn krökt linje, då kommer det att ge en uppfattning om storleken och karaktären av förändringen i den inducerade e. etc. (ström) vid valfri position av ledaren i ett magnetfält. På grund av det faktum att värdet av den inducerade e. etc. p. vid varje ögonblick bestäms av sinus för den vinkel, vid vilken tråden korsar det i fig. visade magnetfältet. 1 kurva kallas en sinusform, och e. etc. s. — sinusformad.

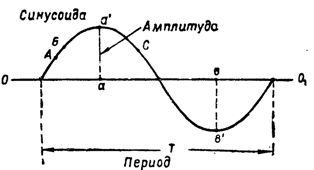
Ris. 2. Sinusformen och dess karakteristiska värden

Förändringarna vi tittade på t.ex. etc. c. sinusformigt motsvarar trådens rotation i ett magnetfält i en vinkel på 360°. När tråden roteras nästa 360°, ändras förändringarna i den inducerade e. etc. s.(och ström) kommer att visas igen i en sinusvåg, det vill säga de kommer att upprepas med jämna mellanrum.

Följaktligen, orsakad av detta e. etc. c. kallas elektrisk ström sinusformad växelström... Det är ganska uppenbart att den spänning som kan mätas av oss vid ändarna av tråd A, i närvaro av en sluten extern krets, också kommer att förändras på ett sinusformigt sätt.

Växelström som erhålls genom att rotera en tråd i ett magnetiskt flöde eller ett system av ledningar kopplade i en spole kallas enfas växelström.

Sinusformade växelströmmar är de mest använda inom tekniken. Däremot kan du hitta växelströmmar som inte ändras enligt sinuslagen. Sådana växelströmmar kallas icke-sinusformade.

Se även: Vad är växelström och hur skiljer den sig från likström

Amplitud, period, frekvens för enfas växelström

Aktuell styrka, förändras längs en sinusform, förändras kontinuerligt. Så, om strömmen i punkt A (fig. 2) är lika med 3a, kommer den redan i punkt B att vara större.Vid någon annan punkt på sinusformen, till exempel vid punkt C, kommer nu strömmen att få ett nytt värde, och så vidare.

Strömmens styrka vid vissa tidpunkter när den ändras längs en sinusform kallas momentana strömvärden.

Det största momentana värdet av en enfas växelström kallas när den ändras längs en sinusformad amplitud... Det är lätt att se att för ett varv av tråden når strömmen sitt amplitudvärde två gånger. Ett av värdena för aa 'är positivt och dras upp från 001-axeln och det andra bv' är negativt och dras ned från axeln.

Den tid under vilken den inducerade e. etc. (eller strömkraften) går igenom hela förändringscykeln, den så kallade månadscykeln T (fig. 2). Perioden mäts vanligtvis i sekunder.

Periodens reciproka kallas frekvensen (f). Med andra ord, växelströmsfrekvens är antalet perioder per tidsenhet, dvs. på sekunder. Så, till exempel, om en växelström inom 1 sekund antar samma värden och riktning tio gånger, kommer frekvensen för en sådan växelström att vara 10 perioder per sekund.

För att mäta frekvensen används istället för antalet perioder per sekund en enhet som kallas hertz (hertz). En frekvens på 1 hertz är lika med en frekvens på 1 lps/sek. Vid mätning av höga frekvenser är det bekvämare att använda en enhet 1000 gånger större än hertz, d.v.s. kilohertz (kHz), eller 1 000 000 gånger större än hertz — megahertz (mhz).

Växelströmmar som används inom teknik, beroende på frekvens, kan delas in i lågfrekventa strömmar och högfrekventa strömmar.

AC rms värde

Likström som passerar genom tråden värmer den. Om du kör växelström genom tråden kommer även tråden att värmas upp.Detta är förståeligt, för även om växelströmmen ändrar sin riktning hela tiden, beror värmeavgivningen inte alls på strömriktningen i tråden.

När växelström passerar genom en glödlampa kommer dess glödtråd att lysa. Vid en standard växelströmsfrekvens på 50 Hz kommer det inte att bli något flimmer av ljuset, eftersom glödlampans glödtråd, som har termisk tröghet, inte har tid att svalna vid de tidpunkter då strömmen i kretsen är noll. Användningen av växelström med en frekvens på mindre än 50 Hz för belysning är nu oönskad på grund av det faktum att obehagliga, ögontröttande fluktuationer i glödlampans intensitet uppstår.

Om vi ​​fortsätter med likströmsanalogin kan vi förvänta oss att en växelström som flyter genom en tråd skapar runt den magnetiskt fält. Egentligen skapar nVäxelström inte ett magnetfält, men eftersom det magnetiska fältet den skapar kommer också att variera i riktning och storlek.

En växelström ändras hela tiden i både magnitud och riktningNS. Naturligtvis uppstår frågan om hur man mäter variabeln T-brunnen, och vad dess värde vid förändring längs en sinusoid bör tas som orsak till den eller den åtgärden.

C För detta ändamål jämförs växelström i termer av verkan den producerar med likström, vars värde förblir oförändrat under experimentet.

Antag att en likström flyter genom en tråd med konstant motstånd 10 A och det visar sig att tråden värms upp till en temperatur på 50 °.Om vi ​​nu passerar genom samma tråd inte en likström, utan en växelström, och så vi väljer dess värde (verkar till exempel med en reostat) så att tråden också värms upp till en temperatur av 50 °, då i detta fall kan vi säga att växelströmmens verkan är lika med likströmsverkan.

Uppvärmning av tråden i båda fallen till samma temperatur visar att på en tidsenhet avger växelströmmen i tråden lika mycket värme som likströmmen.

En sinusformad växelström som för ett givet motstånd per tidsenhet avger samma mängd värme som en likström som i storlek motsvarar en likström... Detta strömvärde kallas det effektiva (Id) eller effektiva värdet av växelström .. Därför, för vårt exempel, kommer det effektiva värdet av växelström att vara 10 A... I det här fallet kommer de maximala (topp) strömvärdena att överstiga medelvärdena i storlek.

Erfarenhet och beräkningar visar att de effektiva värdena för växelström är mindre än dess amplitudvärden i √2 (1,41) gånger. Därför, om toppvärdet för strömmen är känt, så kan det effektiva värdet för strömmen Id bestämmas genom att dividera amplituden för strömmen Ia med √2, dvs. Id = Aza/√2

Omvänt, om rms-värdet för strömmen är känt, kan toppvärdet för strömmen beräknas, dvs. Ia = Azd√2

Samma relationer kommer att gälla för amplituden och rms-värdena för e. etc. v. och spänningar: Enhet = Ea /√2, Ud = Uа/√2

Mätanordningar visar oftast de faktiska värdena, därför utelämnas indexet «d» vanligtvis vid notering, men du bör inte glömma det.

Impedans i AC-kretsar

När induktans- och kapacitansförbrukare är anslutna till AC-kretsen måste både aktiv och reaktans beaktas (reaktans uppstår när en kondensator är på eller choker i en AC-krets). Därför, när man bestämmer strömmen som passerar genom en sådan konsument, är det nödvändigt att dela matningsspänningen med impedansen hos kretsen (konsumenten).

Impedansen (Z) för en enfas AC-krets bestäms av följande formel:

Z = √(R2 + (ωL — 1 / ωC)2

där R är kretsens aktiva resistans i ohm, L är kretsens induktans i henries, C är kapacitansen för kretsen (kondensatorn) i farad, ω — växelströmmens vinkelfrekvens.

Olika konsumenter används i växelströmskretsar där det är nödvändigt att överväga antingen de tre värdena på R, L, C eller bara några av dem. Samtidigt måste man ta hänsyn till växelströmmens vinkelfrekvens.

För vissa användare kan endast värdena för R och L beaktas vid motsvarande hörnfrekvensvärden. Till exempel vid en AC-frekvens på 50 Hz magnetspole eller så kan generatorlindningen endast anses innehålla aktivt och induktivt motstånd. Med andra ord kan kapacitansen i detta fall försummas. Sedan kan AC-impedansen för en sådan användare beräknas med formeln:

Z = √(R2 + ω2L2)

Om en sådan spole eller en spole avsedd för växelströmsdrift kopplas till en likström med samma spänning, kommer en mycket stor ström att flyta genom spolen, vilket kan leda till betydande värmeutveckling, och spolens isolering kan skadas. Tvärtom kommer en liten ström att flyta genom en spole utformad för att fungera i en likströmskrets och ansluten till en växelströmskrets med samma spänning, och enheten i vilken denna spole används kommer inte att utföra den nödvändiga åtgärden.

Motståndstriangel, spänningstriangel och effekttriangel: