Icke-linjära elektriska kretsar
Syfte med icke-linjära element i elektriska kretsar
V elektriska kretsar kan innehålla passiva element, elektrisk resistans vilket i huvudsak beror på strömmen eller spänningen, med resultatet att strömmen inte är direkt proportionell mot spänningen. Sådana element och de elektriska kretsarna i vilka de kommer in kallas icke-linjära element.
Icke-linjära element ger elektriska kretsar egenskaper som är ouppnåeliga i linjära kretsar (spännings- eller strömstabilisering, DC-förstärkning, etc.). De är okontrollerbara och kontrollerade... Den första — bipolära — är utformad för att fungera utan påverkan av en styrfaktor på dem (halvledartermistorer och dioder), och den andra — multipolär — används när en styrfaktor verkar på dem (transistorer) och tyristorer).
Strömspänningsegenskaper för icke-linjära element
De elektriska egenskaperna hos olinjära element är ström-spänningsegenskaper I (U) experimentellt erhållna grafer som visar strömberoendet på spänningen, för vilka en ungefärlig, bekväm för beräkning empirisk formel ibland görs.
Okontrollerade olinjära element har en enda ström-spänningskarakteristik, och kontrollerade olinjära element har en familj av sådana egenskaper vars parameter är den styrande faktorn.
Linjära element har ett konstant elektriskt motstånd, så deras ström-spänningskarakteristik är en rät linje som går genom origo (fig. 1, a).
Ström-spänningsegenskaperna för icke-linjära har en annan form och är indelade i symmetriska och asymmetriska med avseende på koordinataxlarna (fig. 1, b, c).
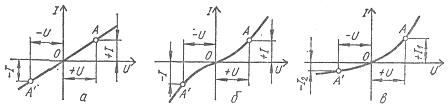
Ris. 1. Strömspänningsegenskaper för passiva element: a — linjär, b — olinjär symmetrisk, c — olinjär asymmetrisk
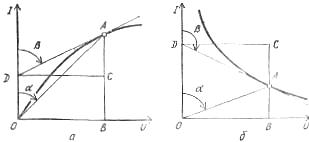
Ris. 2. Grafer för att bestämma den statiska till differentiella resistansen för icke-linjära element i sektionerna av ström-spänningsegenskaperna: a — stigande, b — fallande
För icke-linjära element med en symmetrisk ström-spänningskarakteristik eller för symmetriska element, orsakar en förändring i spänningsriktningen ingen förändring av strömvärdet (fig. 1, b), och för icke-linjära element med en asymmetrisk spänning -strömkarakteristik, eller för asymmetriska element, med ett och samma absolutvärde av spänningen riktad i motsatta riktningar, är strömmarna olika (fig. 1, c). Därför används olinjära symmetriska element i DC- och AC-kretsar, och olinjära obalanserade element, som regel, i AC-kretsar för att omvandla AC till DC-ström.
Egenskaper för icke-linjära element
För varje icke-linjärt element urskiljs ett statiskt motstånd som motsvarar en given punkt av ström-spänningskarakteristiken, till exempel punkt A:
Rst = U/I = muOB/miBA = mr tga
och differentialresistansen som är för. samma punkt A bestäms av formeln:
Rdiff = dU / dI = muDC / miCA = mr tgβ,
där mi, mi, sir — respektive skalan av spänningar, strömmar och resistanser.
Den statiska resistansen kännetecknar egenskaperna hos ett icke-linjärt element i konstantströmsläget, och differentialresistansen - för små avvikelser av strömmen från det stabila tillståndsvärdet. Båda ändras när de går från en punkt och strömspänningskarakteristiken till en annan, den första är alltid positiv och den andra variabeln: i den stigande sektionen av karakteristiken är strömspänningen positiv och i den fallande sektionen är den negativ.
Icke-linjära element kännetecknas också av reciproka värden: statisk konduktivitet Gst och differentiell konduktivitet Golika eller dimensionslösa parametrar —
relativt motstånd:
Kr = — (Rdifference /Rst)
eller relativ konduktivitet:
Kg = — (Gdifference / Gst)
Linjära element har parametrar Kr och Kilogram lika med en, och för icke-linjära element skiljer de sig från det, och ju mer de skiljer sig från en, desto mer manifesteras olinjäriteten hos den elektriska kretsen.
 Beräkning av icke-linjära elektriska kretsar
Beräkning av icke-linjära elektriska kretsar
Icke-linjära elektriska kretsar beräknas grafiskt och analytiskt baserat på Kirchhoffs lagar och volt-ampere-egenskaper för individuella element i växelströmskretsar för omvandling av växelström till likström.
När du grafiskt beräknar en elektrisk krets med två seriekopplade olinjära motstånd R1 och R2 med ström-spänningskarakteristika Iz (U1) och Iz (U2), bygg ström-spänningskarakteristiken för hela kretsen Iz (U), där U = U1 + U2, vars abskiss av punkterna hittas genom att summera abskissorna för punkterna för strömspänningsegenskaperna för olinjära motstånd med lika ordinater (fig. 3, a, b).
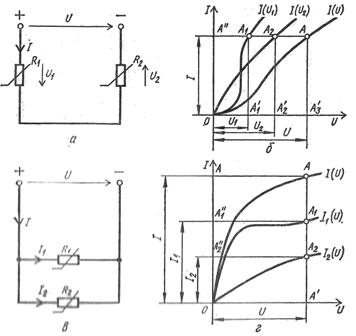
Ris. 3. Diagram och egenskaper för icke-linjära elektriska kretsar: a — seriekopplingskrets av icke-linjära motstånd, b — volt-amperekarakteristika för enskilda element och seriekretsar, c — schema för parallellkoppling av icke-linjära motstånd, d — Volt-amperekarakteristika för enskilda element och en parallellkrets.
Närvaron av denna kurva tillåter spänningen U att hitta strömmen Az såväl som spänningen U1 och U2 vid motståndens anslutningar.
På samma sätt utförs beräkningen av den elektriska kretsen med två parallellkopplade motstånd. R1 och R2 med ström-spänningskarakteristika I1 (U) och Az2 (U), för vilka ström-spänningskarakteristiken för hela kretsen Az(U) byggdes, där Az = I1+I2, på vilken, med en given spänning U, hitta strömmar Az, I1, I2 (oriz. 3, c, d).
Den analytiska metoden för att beräkna icke-linjära elektriska kretsar är baserad på presentationen av spänningsegenskaperna för de icke-linjära elementen genom ekvationerna för motsvarande matematiska funktioner, vilket gör det möjligt att upprätta de nödvändiga tillståndsekvationerna för de elektriska kretsarna .Eftersom lösningen av sådana olinjära ekvationer ofta orsakar betydande svårigheter, är den analytiska metoden för att beräkna olinjära kretsar bekväm när driftssektionerna av ström-spänningsegenskaperna för olinjära element kan rätas ut. Detta gör att du kan beskriva kretsens elektriska tillstånd med linjära ekvationer som inte skapar svårigheter att lösa dem.
Grunderna i elektroteknik:
På potentialskillnad, elektromotorisk kraft och spänning
Elektrisk ström i vätskor och gaser
Elektriskt motstånd hos ledningar
Magnetism och elektromagnetism
Om magnetfältet, solenoider och elektromagneter
Självinduktion och ömsesidig induktion
Elektriskt fält, elektrostatisk induktion, kapacitans och kondensatorer
Vad är växelström och hur skiljer den sig från likström

