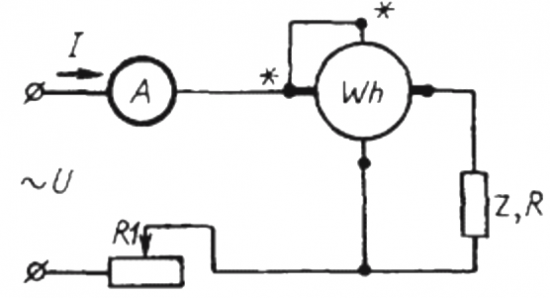
Principen och metoderna för indirekt bestämning av effektfaktorn i växelströmskretsen
Effektfaktor eller cosinus phi, med avseende på användaren av sinusformad växelström, är förhållandet mellan den aktiva effektförbrukningen P och den totala effekten S som tillförs denna användare från nätverket.
Total effekt S, i det allmänna fallet, kan definieras som produkten av de effektiva (root mean square) värdena av strömmen I och spänningen U i den aktuella kretsen, och den aktiva effekten P - som irreversibelt förbrukas av användaren för driften av arbetet.
Reaktiv effekt Q, även om det är en del av den totala effekten, konsumeras det dock inte för att utföra arbete, utan deltar bara i skapandet av alternerande elektriska och magnetiska fält i vissa delar av användarens krets.
bortsett från direkt effektfaktormätning användning av elektrodynamiska anordningar — fasmätare, det finns ganska logiska indirekta metoder som låter dig matematiskt noggrant förstå värdet av denna mycket viktiga elektriska storhet som kännetecknar användaren i en sinusformad växelströmskrets.
Låt oss titta på uppgifterna indirekta metoder i detalj, Låt oss förstå principen för indirekt effektfaktormätning.
Voltmeter, amperemeter och wattmeter metod
Elektrodynamisk wattmätare med ytterligare aktivt motstånd i kretsen för dess rörliga spole indikerar värdet av extremt aktiv effekt som förbrukas i AC-kretsen P.
Om vi nu, med hjälp av en voltmeter och en amperemeter, mäter medelvärdena för strömmen I och spänningen U som verkar i kretsen för den belastning som studeras, så får vi genom att multiplicera dessa två parametrar endast den totala effekten S .
Då kan effektfaktorn (cosinus phi) för en given last lätt hittas med hjälp av formeln:
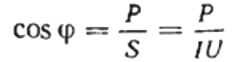
Här, om du så önskar, kan du också hitta värdet på den reaktiva effekten Q, det totala motståndet för kretsen z Ohms lag, såväl som aktivt och reaktivt motstånd, helt enkelt genom att konstruera eller representera en motståndstriangel och sedan använda Pythagoras sats:
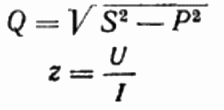
Räknare och amperemeter metod
För att använda denna metod är det nödvändigt att montera en krets där den enklaste är ansluten i serie med belastningen Z och amperemetern elmätare Wh.
Under en viss tidsperiod t, i storleksordningen en minut, kommer det att vara nödvändigt att beräkna antalet varv på skivan N, vilket kommer att visa mängden aktiv energi som spenderas under en given tid (dvs. effektfaktor).
Här: antalet varv på skivan N, koefficienten k är mängden energi per varv, I och U är rms ström respektive spänning, t är tiden för att räkna varven, cosinus phi är effektfaktorn:
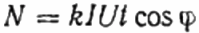
Sedan, istället för den studerade användaren Z, ingår den aktiva belastningen R i kretsen genom samma räknare, men inte direkt, utan genom reostaten R1 (att uppnå samma ström I som i det första fallet, med användaren Z). Antalet varv för skivan N1 bibehålls under samma tid t. Men här, eftersom belastningen är aktiv, är cosinus phi (effektfaktor) verkligen lika med 1. Därför:
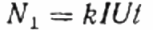
Därefter registreras förhållandet mellan varv för skivräknaren under samma tidsperiod i det första och andra fallet. Detta kommer att vara cosinus phi, det vill säga effektfaktorn för den första belastningen (i förhållande till en rent aktiv belastning med samma nuvarande):
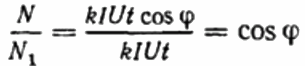
Metod med tre amperemeter
För att bestämma effektfaktorn i en sinusformad strömkrets med hjälp av tre amperetrar måste du först montera följande krets:
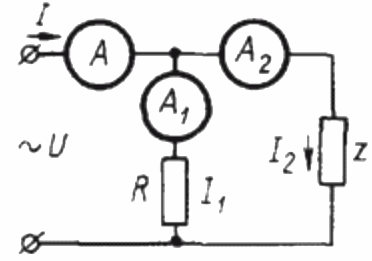
Här är Z en last vars effektfaktor ska bestämmas och R är en rent aktiv last.
Eftersom belastningen R är enbart aktiv är strömmen I1 vid varje tidpunkt i fas med växelspänningen U. I detta fall är strömmen I lika med den geometriska summan av strömmarna I1 och I2. Nu kommer vi baserat på denna position att bygga ett vektordiagram av strömmarna:
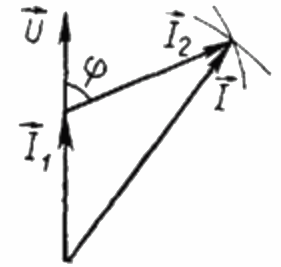
På vektordiagrammet för strömmarna är den spetsiga vinkeln mellan strömmen I1 och strömmen I2 vinkeln phi, vars cosinus (i själva verket värdet på effektfaktorn) kan hittas från en speciell värdetabell trigonometriska funktioner eller beräknas med formeln:
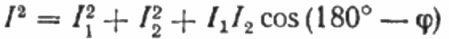
Härifrån kan vi uttrycka cosinus phi, det vill säga den önskade effektfaktorn:
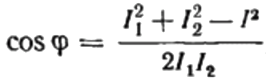
Tecknet för den hittade effektfaktorn («+» eller «-«) kommer att indikera belastningens art. Om effektfaktorn (cosinus phi) är negativ är belastningen kapacitiv till sin natur. Om effektfaktorn är ett positivt värde, är belastningens natur induktiv.