Kretstopologier—Grundläggande koncept

En elektrisk krets är en uppsättning enheter (element) och deras anslutningstrådar genom vilka en elektrisk ström kan flöda. Alla delar av elektriska kretsar delar i passiv och aktiv.

Aktiva element omvandlar olika typer av energi (mekanisk, kemisk, ljus, etc.) till elektrisk energi. I passiva enheter omvandlas elektrisk energi till andra typer av energi. Aktiva element kallas källor, passiva kallas konsumenter eller mottagare.

I kretsteorin övervägs idealiserade modeller av elektriska element. Detta gör beskrivningen av elementen så enkel som möjligt. Mer komplexa, verkliga element är modellerade från en uppsättning idealiserade element.

De huvudsakliga passiva elementen i elektriska kretsar är resistor (resistivt element), induktor (induktivt element) och kondensator (kapacitivt element). Element installeras i en elektrisk krets för att generera spänning och ström av ett givet värde och form (se — Elektrisk krets och dess element).

En elektrisk krets består av grenar och noder. Gren — detta är en del av en elektrisk krets (krets) genom vilken samma ström flyter. En knut — Anslutning av tre eller flera grenar. På det elektriska diagrammet indikeras noden med en punkt (fig. 1).

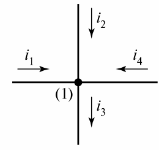
Ris. 1. Definiera noden i diagrammet

Vid behov numreras diagrammets noder från vänster till höger uppifrån och ned.

I fig. 2 visar den resistiv-kapacitiva grenen i vilken strömmen iC flyter.

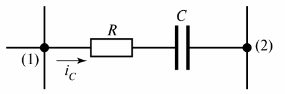
Ris. 2. Resistiv-kapacitiv gren

En annan definition av en gren kan ges — det är en sektion av en krets mellan två intilliggande noder (noder (1) och (2) i fig. 2).

Kedja Finns det någon stängd bana i den elektriska kretsen. Kretsen kan stängas av alla grenar, inklusive villkorliga grenar vars motstånd är lika med oändlighet.

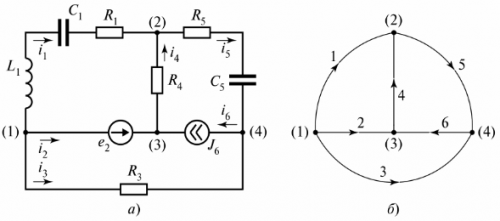
I fig. 3 visar en grenad elektrisk krets som består av tre grenar.

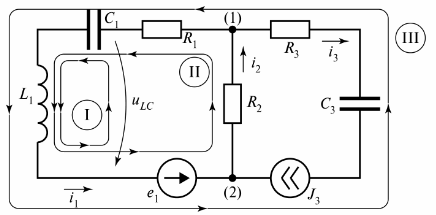
Ris. 3. Elektrisk krets med två kretsar

Diagrammet visar tre kretsar, och krets I är sluten av en gren med oändligt motstånd. Denna gren indikeras som spänning tiLC.

För kretsen i fig. 3 är det möjligt att komponera många slingor som är slutna av verkliga eller villkorade grenar, men för beräkningen av elektriskt brus används begreppet "oberoende slinga". Antalet oberoende kretsslingor ställs alltid in som det minimum som krävs för beräkningen.

Oberoende kretsar är alltid slutna, men grenar som har ett motstånd som inte är lika med oändlighet, och varje oberoende krets inkluderar minst en gren som inte ingår i andra kretsar. För komplexa elektriska kretsar kan du bestämma antalet oberoende kretsar med hjälp av kretsschemat.

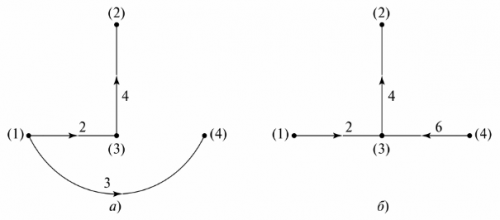
På kretsschemat en villkorlig representation av kretsen kallas, där varje gren ersätts av ett linjesegment. Objekt i grenar visas inte. Till exempel, i FIG. 4 visar en grenkrets och dess diagram.

Ris. 4. Förgrenad elektrisk krets: a — kretsschema, b — diagram

För att göra ett diagram över ett diagram måste du ansluta noderna med grenlinjer utan att ange element på dem. Grenarna är numrerade och riktningarna för strömmarna på dem indikeras med pilar. Grafen i sig har ingen fysisk betydelse, men kan användas för att bestämma antalet och typen av oberoende konturer. För detta ändamål förbereds ett "grafiskt träd".

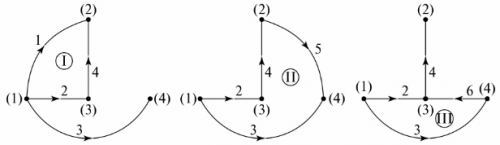
Grafiskt träd Den representerar grafen för en krets vars noder är anslutna av grenar på ett sådant sätt att ingen sluten slinga uppstår. Det kan finnas flera alternativ för att visa ett grafiskt träd. I fig. 5 visar två möjliga alternativ för kretsen i FIG. 4.

Ris. 5. Schemats grafiska träd

Antalet saknade grenar i grafträdet är lika med antalet oberoende slingor i kretsen. I exemplet är dessa tre grenar, tre oberoende loopar. Konfigurationen av oberoende loopar kan erhållas genom att sekventiellt koppla samman grafträdets noder med grenar som inte är specificerade i grafträdet. Till exempel, för grafträdet i fig. 5, och de oberoende konturerna visas i fig. 6.

Ris. 6. Bestämma oberoende konturer genom grafträdet

Valet av ett alternativ för att konfigurera oberoende kretsar för beräkning av kretsen utförs under kretsanalys. Du bör välja sådana konturer så att beräkningen är så enkel som möjligt, d.v.s. antalet beroende ekvationer i systemet är minimalt.

Topologiska ekvationer etablerar ett samband mellan spänningar och strömmar i en krets, och antalet och typen av ekvationer beror inte på vilka element som ingår i grenarna. Topologiska ekvationer inkluderar ekvationer som består av enligt Kirchhoffs lagar.