Oscillerande process inom elektroteknik och elektronik, typer av svängningar
Oscillerande process — en process med olika grader av repeterbarhet. Alla oscillerande processer är indelade i 2 klasser: periodiska och icke-periodiska. I teorin använder de också en mellanklass - nästan periodiska svängningar.
En oscillerande process kallas periodisk, där värdet som kännetecknar denna process, taget när som helst, efter en viss tidsperiod T har samma värde.
Funktionen f (t), som är ett matematiskt uttryck för den oscillerande processen, kallas periodisk med period T om den uppfyller villkoret f (t + T) = f (t).
Bland klassen av periodiska oscillerande processer spelas huvudrollen av harmoniska eller sinusformade svängningar, där en förändring i en fysisk kvantitet med tiden sker enligt sinus- eller cosinuslagen. Deras totala rekord är:
y = f (t) = aCos ((2π / T) t — φ),
där a — svängningarnas amplitud, φ är svängningsfasen, 1 /T = f — frekvensen och 2πf = ω — frekvensen av cykliska eller cirkulära vibrationer.
Tillämpning av sinusformade oscillationer och deras egenskaper:
Grundläggande parametrar för AC
Grafiska sätt att visa växelström
En nästan periodisk funktion som motsvarar en avläsning av periodiska svängningar definieras av villkoret:
| f · (t + τ) — f (t) | <= ε där ε — tilldela ett värde till varje värde T.
Kvantiteten τ detta fall kallas nästan period. Om värdet ε är mycket litet jämfört med medelvärdet av f (t) vid tidpunkten T, kommer den kvasi-periodiska funktionen att vara nära den periodiska.
Icke-periodiska svängningar är mycket mer varierade än periodiska. Men oftast inom automation måste man möta dämpning eller ökande sinusformade svängningar.
Svängningar enligt lagen om den dämpade sinusformen eller, som de ibland kallas, dämpade harmoniska svängningar, kan representeras i en allmän form:
x = Ae-δTcos·(ω + φ),
där t är tid, A och φ är godtyckliga konstanter. Den allmänna notationen av lagen om ökande harmoniska svängningar skiljer sig endast i tecknet på dämpningsfaktorn δ[1 sekund].
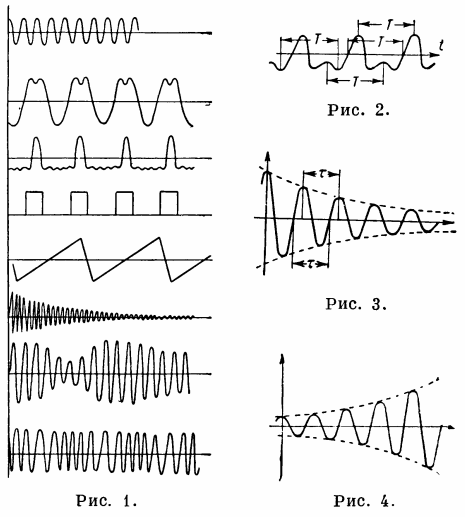
Fikon. 1 — oscillerande process, fig. 2. — periodisk process, fig. 3. — sönderfallande harmoniska svängningar, fig. 4. — ökning av harmoniska svängningar.
Ett exempel på tillämpningen av den oscillerande processen är den enklaste oscillerande kretsen.
Oscillatorkrets (elektrisk krets) - en passiv elektrisk krets där elektriska svängningar kan uppstå med en frekvens som bestäms av parametrarna för själva kretsen.
Den enklaste oscillerande kretsen består av kapacitans C och induktans L. I frånvaro av yttre påverkan, dämpande svängningar med frekvensen εО = 1/2π√LC.
Vibrationernas amplitud minskar med t.ex.-δT, där δ är dämpningskoefficienten. Om δ> = eO blir de dämpade svängningarna i kretsen icke-periodiska.
Inom elektroniken bestäms kvaliteten på den oscillerande kretsen av kvalitetsfaktorn: Q = nf/δ... När en extern periodisk kraft verkar på den oscillerande kretsen uppstår tvångssvängningar i den. Amplituden för forcerade svängningar ökar avsevärt för hög-Q-kretsar om frekvensen för den yttre påverkan är nära eo (resonans). Oscillerande krets är en av huvuddelarna i resonansförstärkare, generatorer och andra elektroniska apparater.
Se även om detta ämne: Tillämpning av spänningsresonans och strömresonans
