Vad är inre motstånd

Antag att det finns en enkel elektrisk sluten krets som inkluderar en strömkälla, till exempel en generator, galvanisk cell eller batteri, och ett motstånd med motståndet R. Eftersom strömmen i kretsen inte bryts någonstans flyter den också inuti källan.

I en sådan situation kan vi säga att varje källa har ett visst internt motstånd som hindrar strömmen från att flyta. Detta interna motstånd kännetecknar strömkällan och betecknas med bokstaven r. För galvanisk cell eller batteri, det interna motståndet är motståndet hos elektrolytlösningen och elektroderna, för en generator - resistansen hos statorlindningarna, etc.

Således kännetecknas en strömkälla av både storleken på EMF och värdet på dess eget inre motstånd r — båda egenskaperna indikerar källans kvalitet.

Högspänningselektrostatiska generatorer (som Van de Graaf-generatorn eller Wimshurst-generatorn) har till exempel en enorm EMF mätt i miljoner volt, medan deras inre resistans mäts i hundratals megohm, så de är inte lämpliga för att erhålla höga strömmar.

Tvärtom har galvaniska celler (som ett batteri) en EMF i storleksordningen 1 volt, även om deras inre motstånd är av storleksordningen bråkdelar eller högst tio ohm, och därför kan strömmar av enheter och tiotals ampere erhållas från galvaniska celler.

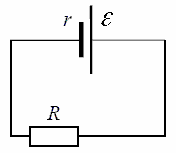
Detta diagram visar en verklig källa med en ansluten last. De definieras här EMF-källa, dess inre motstånd såväl som belastningsmotstånd. Enligt Ohms lag för en sluten krets, strömmen i denna krets kommer att vara lika med:

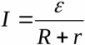
Eftersom den externa kretssektionen är homogen, kan spänningen över lasten hittas från Ohms lag:

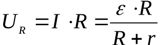
Genom att uttrycka belastningens motstånd från den första ekvationen och ersätta dess värde i den andra ekvationen, får vi beroendet av spänningen i belastningen på strömmen i en sluten krets:

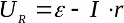
I en sluten slinga är EMF lika med summan av spänningsfallet på de externa kretselementen och på själva källans inre resistans. Beroendet av belastningsspänningen på belastningsströmmen är idealiskt linjärt.

Grafen visar detta, men experimentdata för ett riktigt motstånd (korsar nära grafen) skiljer sig alltid från idealet:

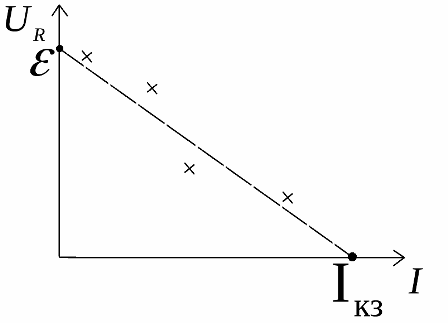
Experiment och logik visar att vid nollbelastningsström är den externa kretsspänningen lika med källemk och vid nolllastspänning är kretsströmmen kortslutning ström… Denna egenskap hos verkliga kretsar hjälper till att experimentellt hitta EMF och inre resistans hos verkliga källor.

Experimentell detektering av internt motstånd

För att experimentellt bestämma dessa egenskaper byggs en graf över spänningens beroende av belastningen av strömmens storlek, varefter den extrapoleras till skärningspunkten med axlarna.

Vid skärningspunkten för grafen med spänningsryggraden är värdet på källans emk, och vid skärningspunkten med strömaxeln är värdet på kortslutningsströmmen. Som ett resultat hittas det inre motståndet av formeln:

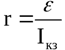
Den användbara kraften som utvecklas av källan fördelas över lasten. Grafen över denna effekts beroende av belastningsmotståndet visas i figuren. Denna kurva startar från skärningspunkten mellan koordinataxlarna vid nollpunkten, stiger sedan till maximalt effektvärde och faller sedan till noll med ett belastningsmotstånd lika med oändligt.

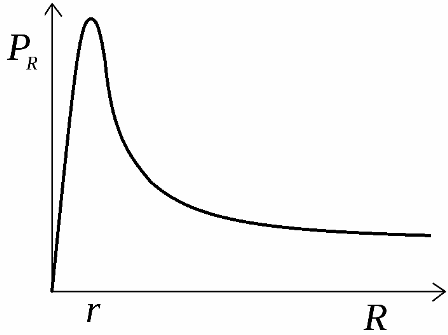
För att hitta den maximala belastningsresistansen vid vilken teoretisk maximal effekt kommer att utvecklas med en given källa, tas derivatan av effektformeln med avseende på R och sätts till noll. Maximal effekt kommer att utvecklas när den externa kretsresistansen är lika med den interna källresistansen:

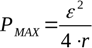
Denna bestämmelse för den maximala effekten vid R = r gör att du experimentellt kan hitta källans inre resistans genom att plotta den kraft som frigörs vid belastningen kontra värdet på belastningsresistansen.Att hitta ett faktiskt snarare än teoretiskt belastningsmotstånd som ger maximal effekt bestämmer det faktiska interna motståndet hos strömförsörjningen.

Strömkällans verkningsgrad anger förhållandet mellan den maximala effekten fördelad på lasten och den totala effekten som för närvarande utvecklas

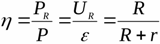
Det är klart att om källan utvecklar sådan effekt att den maximala möjliga effekten för en given källa erhålls vid belastningen, så kommer källans verkningsgrad att vara lika med 50%.