Kortslutningsström, som bestämmer storleken på kortslutningsströmmen

Den här artikeln kommer att fokusera på kortslutningar i elektriska nätverk. Vi kommer att överväga typiska exempel på kortslutningar, metoder för att beräkna kortslutningsströmmar, uppmärksamma förhållandet mellan induktivt motstånd och transformatorernas märkeffekt vid beräkning av kortslutningsströmmar, och även ge specifika enkla formler för dessa beräkningar.

Vid design av elektriska installationer är det nödvändigt att känna till värdena för symmetriska kortslutningsströmmar för olika punkter i en trefaskrets. Värdena för dessa kritiska symmetriska strömmar gör det möjligt att beräkna parametrarna för kablar, ställverk, selektiva skyddsanordningar etc.

Överväg sedan en trefas noll-resistans kortslutningsström som matas genom en typisk distributionstransformator. Under normala förhållanden är denna typ av skada (kortslutning av bultanslutningen) den farligaste och beräkningen är mycket enkel.Enkla beräkningar tillåter, med förbehåll för vissa regler, att erhålla tillräckligt exakta resultat som är acceptabla för konstruktion av elektriska installationer.

Kortslutningsström i sekundärlindningen på en nedtrappad distributionstransformator. Som en första approximation antas motståndet i högspänningskretsen vara mycket liten och kan därför försummas:

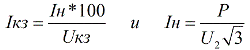
Här är P märkeffekten i volt-ampere, U2 är fas-till-fas-spänningen för sekundärlindningen utan belastning, In är märkströmmen i ampere, Isc är kortslutningsströmmen i ampere, Usc är kortslutningsströmmen i ampere. kretsspänning i procent.

Tabellen nedan visar typiska kortslutningsspänningar för trefastransformatorer för en 20 kV HV-lindning.

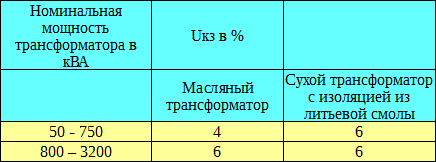
Om vi ​​till exempel betraktar fallet när flera transformatorer matas parallellt med bussen, kan värdet på kortslutningsströmmen i början av linjen som är ansluten till bussen tas lika med summan av kortslutningen strömmar, som tidigare beräknats separat för var och en av transformatorerna.

När alla transformatorer matas från samma högspänningsnät kommer kortslutningsströmmarnas värden, när de summeras, att ge ett något högre värde än vad de faktiskt ser ut. Resistansen hos samlingsskenor och omkopplare försummas.

Låt transformatorn ha en märkeffekt på 400 kVA, spänningen på sekundärlindningen är 420 V, då om vi tar Usc = 4%, då:

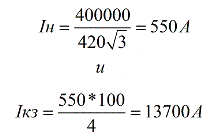
Bilden nedan ger en förklaring till detta exempel.

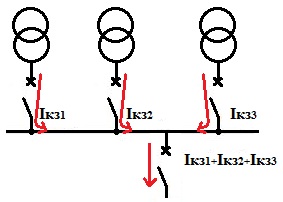
Noggrannheten hos det erhållna värdet kommer att vara tillräcklig för att beräkna den elektriska installationen.

Trefas kortslutningsström vid valfri installationspunkt på lågspänningssidan:

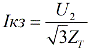
Här: U2 är tomgångsspänningen mellan faserna i transformatorns sekundärlindningar. Zt — impedans för kretsen ovanför felpunkten. Tänk sedan på hur du hittar Zt.

Varje del av installationen, oavsett om det är ett nätverk, en strömkabel, själva transformatorn, en effektbrytare eller en samlingsskena, har sin egen impedans Z bestående av aktiv R och reaktiv X.

Kapacitivt motstånd spelar ingen roll här. Z, R och X uttrycks i ohm och beräknas som sidorna av en rätvinklig triangel som visas i figuren nedan. Impedansen beräknas enligt den rätvinkliga triangelregeln.

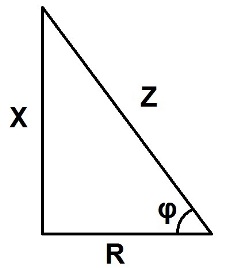
Rutnätet är uppdelat i separata sektioner för att hitta X och R för varje sektion så att beräkningen är bekväm. För en seriekrets läggs resistansvärdena helt enkelt till och resultatet är Xt och RT. Det totala motståndet Zt bestäms av Pythagoras sats för en rätvinklig triangel med formeln:

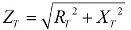
När sektionerna är parallellkopplade utförs beräkningen som för parallellkopplade motstånd, om de kombinerade parallella sektionerna har reaktans eller aktivt motstånd erhålls motsvarande totala resistans:

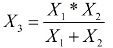
Xt tar inte hänsyn till påverkan av induktanser, och om intilliggande induktanser påverkar varandra, kommer den faktiska induktansen att vara högre. Det bör noteras att beräkningen av Xz endast är relaterad till en separat oberoende krets, det vill säga också utan inverkan av ömsesidig induktans. Om de parallella kretsarna är placerade nära varandra, kommer motståndet Xs att vara märkbart högre.

Betrakta nu nätverket som är anslutet till ingången på nedtrappningstransformatorn. Den trefasiga kortslutningsströmmen Isc eller kortslutningseffekt Psc bestäms av elleverantören, men utifrån dessa data kan den totala ekvivalenta resistansen hittas. Ekvivalent impedans, som samtidigt resulterar i ekvivalenten för lågspänningssidan:

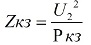
Psc-trefas kortslutningsförsörjning, U2-nolastspänning för lågspänningskretsen.

Som regel är den aktiva komponenten av motståndet i ett högspänningsnätverk - Ra - mycket liten och, jämfört med det induktiva motståndet, obetydlig. Konventionellt tas Xa lika med 99,5% av Za och Ra är lika med 10% av Xa. Tabellen nedan visar ungefärliga siffror för dessa värden för 500 MVA och 250 MVA transformatorer.

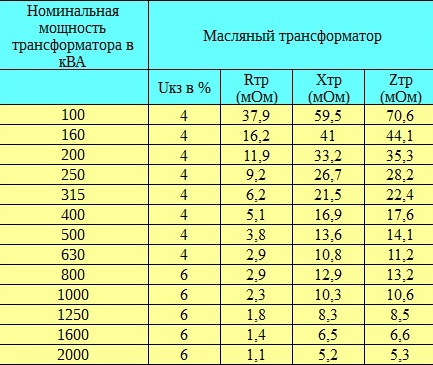
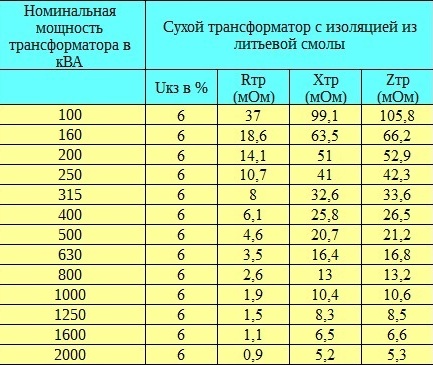
Full Ztr — Lågspänning sidotransformatormotstånd:

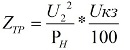
Pn — transformatorns märkeffekt i kilovolt-ampere.

Det aktiva motståndet hos lindningarna baseras på effektförluster.

När man utför ungefärliga beräkningar försummas Rtr och Ztr = Xtr.

Om en lågspänningsbrytare ska övervägas, beaktas effektbrytarens impedans över kortslutningspunkten. Det induktiva motståndet tas lika med 0,00015 Ohm per omkopplare och den aktiva komponenten försummas.

När det gäller samlingsskenorna är deras aktiva motstånd försumbart litet, medan den reaktiva komponenten fördelas med cirka 0,00015 Ohm per meter av deras längd, och när avståndet mellan samlingsskenorna fördubblas ökar deras reaktans med endast 10%. Kabelparametrar specificeras av deras tillverkare.

När det gäller en trefasmotor går den i kortslutningsögonblicket i generatorläge, och kortslutningsströmmen i lindningarna uppskattas till Isc = 3,5 * In. I enfasmotorer är ökningen av strömmen vid kortslutningsögonblicket försumbar.

Bågen som vanligtvis följer med en kortslutning har ett motstånd som inte på något sätt är konstant, men dess medelvärde är extremt lågt, men spänningsfallet över bågen är litet, därför minskar strömmen praktiskt taget med cirka 20%, vilket underlättar driften brytaren utan att störa dess funktion utan att särskilt påverka utlösningsströmmen.

Kortslutningsströmmen vid ledningens mottagande ände är relaterad till kortslutningsströmmen vid ledningens matande ände, men även de sändande ledningarnas tvärsnitt och material samt deras längd beaktas. konto. Med en idé om motstånd kan vem som helst göra denna enkla beräkning. Vi hoppas att vår artikel var användbar för dig.