Trianglar av spänningar, resistanser och effekter

Alla som har en idé om vektordiagram kommer lätt att märka att en rätvinklig spänningstriangel mycket tydligt kan urskiljas på dem, vars sida reflekterar: kretsens totala spänning, spänningen för det aktiva motståndet och spänningen på reaktans.

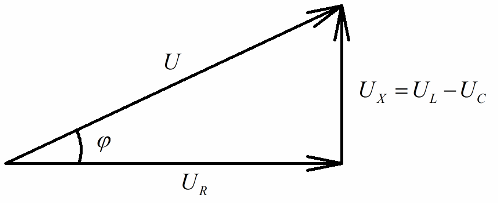
I enlighet med Pythagoras sats kommer förhållandet mellan dessa spänningar (mellan kretsens totala spänning och spänningen i dess sektioner) att se ut så här:

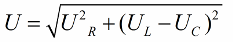
Om nästa steg är att dividera värdena för dessa spänningar med strömmen (strömmen flyter lika genom alla sektioner av seriekretsen), Ohms lag vi får motståndsvärdena, det vill säga nu kan vi prata om en rätvinklig triangel av motstånd:

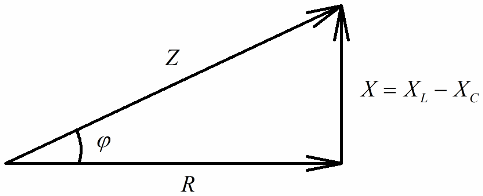
På ett liknande sätt (som i fallet med spänningar), med hjälp av Pythagoras sats, är det möjligt att fastställa ett samband mellan kretsens impedans och reaktanserna. Relationen kommer att uttryckas med följande formel:

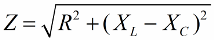
Sedan multiplicerar vi motståndsvärdena med strömmen, i själva verket kommer vi att öka varje sida av den räta triangeln med ett visst antal gånger. Som ett resultat får vi en rätvinklig triangel med kapacitet:

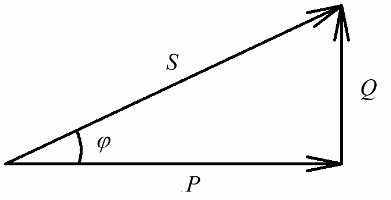
Den aktiva effekten som frigörs vid kretsens aktiva motstånd i samband med den irreversibla omvandlingen av elektrisk energi (till värme, vid utförandet av arbete i installationen) kommer att vara tydligt relaterad till den reaktiva effekten som är involverad i den reversibla omvandlingen av energi (skapandet av magnetiska och elektriska fält i spolar och kondensatorer) och med full effekt tillförd den elektriska installationen.

Aktiv effekt mäts i watt (W), reaktiv effekt — i varis (VAR — volt-ampere reactive), totalt — i VA (volt-ampere).

Enligt Pythagoras sats har vi rätt att skriva:

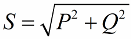
Låt oss nu uppmärksamma det faktum att det i potenstriangeln finns en vinkel phi, vars cosinus är lätt att bestämma främst med aktiv kraft och skenbar kraft. Cosinus för denna vinkel (cos phi) kallas effektfaktor. Den visar hur mycket av den totala effekten som står för när man gör nyttigt arbete i en elinstallation och inte återförs till nätet.

Uppenbarligen indikerar en högre effektfaktor (maximalt en) en högre omvandlingseffektivitet för den energi som levereras till anläggningen för drift. Om effektfaktorn är 1 används all tillförd energi för att utföra arbete.

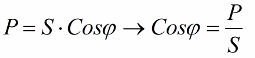
De erhållna förhållandena tillåter uttryck för installationens strömförbrukning i termer av effektfaktor, aktiv effekt och nätverksspänning:

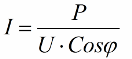
Så ju mindre cosinus phi, desto mer ström krävs av nätverket för att utföra ett visst jobb. I praktiken begränsar denna faktor (maximal nätverksström) överföringskapaciteten för transmissionsledningen och därför, ju lägre effektfaktor, desto större linjebelastning och desto lägre användbar bandbredd (den låga cosinus phi leder till begränsning). Jouleförluster i kraftledningar med minskande cosinus phi kan ses från följande formel:

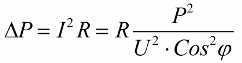
På överföringsledningens aktiva motstånd R ökar förlusterna ju mer ju högre ström I är, trots att den är reaktiv mot belastningen. Därför kan vi säga att med en låg effektfaktor ökar helt enkelt kostnaden för elöverföring. Detta innebär att att öka cosinus phi är en viktig nationell ekonomisk uppgift.

Det är önskvärt att den reaktiva komponenten av den totala effekten ska närma sig noll. För att göra detta skulle det vara bra att alltid använda elmotorer och transformatorer vid full belastning och stänga av dem i slutet av användningen så att de inte går på tomgång. Vid tomgång har motorer och transformatorer en mycket låg effektfaktor. Ett sätt att öka cosinus phi hos användare är att använda kondensatorbanker och synkrona kompensatorer.