AC kondensator

Låt oss sätta ihop kretsen med kondensator, där generatorn genererar en sinusformad spänning. Låt oss analysera sekventiellt vad som kommer att hända i kretsen när vi stänger omkopplaren. Vi kommer att överväga det första ögonblicket när generatorspänningen är lika med noll.

Under periodens första kvartal kommer spänningen över generatorterminalerna att öka, från noll, och kondensatorn börjar laddas. En ström kommer att dyka upp i kretsen, men i det första ögonblicket av laddning av kondensatorn, trots att spänningen på dess plattor precis har dykt upp och fortfarande är mycket liten, kommer strömmen i kretsen (laddningsström) att vara den största . När laddningen på kondensatorn ökar, minskar strömmen i kretsen och når noll i det ögonblick då kondensatorn är fulladdad. I det här fallet blir spänningen på kondensatorns plattor, strikt efter generatorns spänning, i detta ögonblick maximal, men med motsatt tecken, det vill säga den riktas till generatorns spänning.

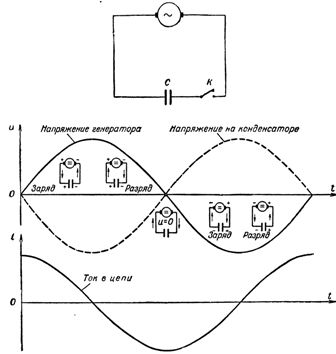
Ris. 1. Ändring av ström och spänning i en krets med kapacitans

På detta sätt rusar strömmen med den största kraften in i en kondensator gratis, men börjar omedelbart minska när plattorna på kondensatorn är fyllda med laddningar och faller till noll och laddar den helt.

Låt oss jämföra detta fenomen med vad som händer med flödet av vatten i ett rör som förbinder två kommunicerande kärl (fig. 2), varav det ena är fullt och det andra tomt. Man behöver bara trycka på ventilen som blockerar vattenvägen, eftersom vatten omedelbart forsar från det vänstra kärlet under stort tryck genom röret in i det tomma högra kärlet. Omedelbart kommer dock vattentrycket i röret att gradvis börja försvagas på grund av utjämningen av nivåerna i kärlen och kommer att sjunka till noll. Vattenflödet kommer att stanna.

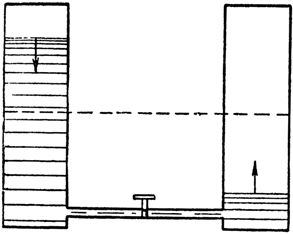
Ris. 2. Förändringen i vattentrycket i röret som förbinder kommunikationskärlen liknar förändringen i strömmen i kretsen under laddningen av kondensatorn

På samma sätt rusar strömmen först in i en oladdad kondensator och försvagas sedan gradvis när den laddas.

När den andra fjärdedelen av perioden börjar, när generatorspänningen initialt startar långsamt och sedan minskar mer och snabbare, kommer den laddade kondensatorn att laddas ur till generatorn, vilket orsakar en urladdningsström i kretsen. När generatorspänningen minskar laddas kondensatorn ur mer och mer och urladdningsströmmen i kretsen ökar. Riktningen för urladdningsströmmen under denna fjärdedel av perioden är motsatt riktningen för laddningsströmmen under periodens första kvartal. Följaktligen är den aktuella kurvan som passerat nollvärdet nu placerad under tidsaxeln.

I slutet av den första halvcykeln närmar sig generatorspänningen, såväl som kondensatorspänningen, snabbt noll och kretsströmmen når långsamt sitt maximala värde. Med tanke på att värdet på strömmen i kretsen är större, ju större värdet på laddningen som bärs i kretsen är, kommer det att bli tydligt varför strömmen når sitt maximum när spänningen på plattorna på kondensatorn, och därför laddningen på kondensator, minskar snabbt.

I början av det tredje kvartalet av perioden börjar kondensatorn laddas igen, men polariteten på dess plattor, liksom generatorns polaritet, ändras "och vice versa, och strömmen fortsätter att flyta i samma riktning, börjar minska när kondensatorn laddas. I slutet av tredje kvartalet av perioden, när generator- och kondensatorspänningarna når sitt maximum, går strömmen till noll.

Under den sista fjärdedelen av perioden faller spänningen, minskande, till noll, och strömmen, efter att ha ändrat sin riktning i kretsen, når sitt maximala värde. Här slutar perioden, varefter nästa börjar, exakt upprepande av föregående osv.

Således, under inverkan av generatorns växelspänning, laddas kondensatorn två gånger under perioden (periodens första och tredje kvartal) och urladdas två gånger (periodens andra och fjärde kvartal). Men eftersom de växlar en efter en kondensatorladdningar och -urladdningar åtföljs varje gång av passagen av laddnings- och urladdningsströmmen genom kretsen, då kan vi dra slutsatsen att växelström.

Du kan kontrollera detta i följande enkla experiment. Anslut en 4-6 mikrofarad kondensator till elnätet via en 25 W glödlampa.Ljuset kommer att tändas och slocknar inte förrän kretsen är bruten. Detta tyder på att en växelström har passerat genom kretsen med kapacitansen. Naturligtvis passerar den inte genom kondensatorns dielektrikum, utan representerar när som helst en laddningsström eller en kondensatorurladdningsström.

Som vi vet är dielektrikumet polariserat under inverkan av ett elektriskt fält som uppstår i det när kondensatorn laddas, och dess polarisering försvinner när kondensatorn laddas ur.

I detta fall tjänar dielektrikumet med förskjutningsströmmen som uppstår i den för växelströmmen som en slags fortsättning av kretsen, och för konstanten bryter den kretsen. Men förskjutningsströmmen bildas endast inom kondensatorns dielektrikum, och därför sker inte överföringen av laddningar längs kretsen.

Resistansen som erbjuds av en AC-kondensator beror på värdet på kondensatorns kapacitans och strömfrekvensen.

Ju större kapacitet kondensatorn har, desto större laddning på kretsen under laddning och urladdning av kondensatorn och följaktligen desto större ström i kretsen. En ökning av strömmen i kretsen indikerar att dess motstånd har minskat.

Därför, när kapacitansen ökar, minskar kretsens motstånd mot växelström.

Det växer aktuell frekvens ökar mängden laddning som bärs i kretsen eftersom laddningen (liksom urladdningen) av kondensatorn måste ske snabbare än vid låg frekvens. Samtidigt motsvarar en ökning av mängden överförd laddning per tidsenhet en ökning av strömmen i kretsen och därför en minskning av dess motstånd.

Om vi ​​på något sätt gradvis minskar växelströmmens frekvens och minskar strömmen till likström, kommer motståndet hos kondensatorn som ingår i kretsen gradvis att öka och bli oändligt stor (bryter kretsen) tills den dyker upp i konstantströmkrets.

Därför, när frekvensen ökar, minskar kondensatorns motstånd mot växelström.

Precis som resistansen hos en spole mot en växelström kallas induktiv, kallas resistansen hos en kondensator kapacitiv.

Därför är det kapacitiva motståndet större, ju lägre kapacitet kretsen har och frekvensen på strömmen som matar den.

Kapacitiv resistans betecknas som Xc och mäts i ohm.

Det kapacitiva motståndets beroende av strömfrekvensen och kretsens kapacitet bestäms av formeln Xc = 1 /ωC, där ω är en cirkulär frekvens lika med produkten av 2πe, C är kretsens kapacitet i farads.

Kapacitivt motstånd, liksom induktivt motstånd, har en reaktiv natur, eftersom kondensatorn inte förbrukar energin från strömkällan.

formel Ohms lag för en kapacitiv krets har den formen I = U / Xc, där I och U - effektiva värden för ström och spänning; Xc är kretsens kapacitiva resistans.

Kondensatorernas egenskap att ge högt motstånd mot lågfrekventa strömmar och att enkelt passera högfrekventa strömmar används ofta i kommunikationsutrustningskretsar.

Med hjälp av kondensatorer, till exempel, uppnås separation av konstanta strömmar och lågfrekventa strömmar från högfrekventa strömmar, nödvändiga för driften av kretsarna.

Om det är nödvändigt att blockera vägen för lågfrekvent ström i den högfrekventa delen av kretsen, är en liten kondensator ansluten i serie. Den ger stort motstånd mot lågfrekvent ström och passerar samtidigt lätt högfrekvent ström.

Om det är nödvändigt att förhindra högfrekvent ström, till exempel i radiostationens kraftkrets, används en kondensator med stor kapacitet, parallellkopplad med strömkällan. I det här fallet passerar högfrekvent ström genom kondensatorn och kringgår radiostationens strömförsörjningskrets.

Aktivt motstånd och kondensator i AC-kretsen

I praktiken observeras ofta fall i en seriekrets med en kapacitans aktivt motstånd ingår. Kretsens totala motstånd i detta fall bestäms av formeln

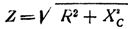
Därför är den totala resistansen för en krets bestående av aktiv och kapacitiv växelströmsresistans lika med kvadratroten av summan av kvadraterna av den aktiva och kapacitiva resistansen för denna krets.

Ohms lag förblir giltig för denna I = U / Z-krets också.

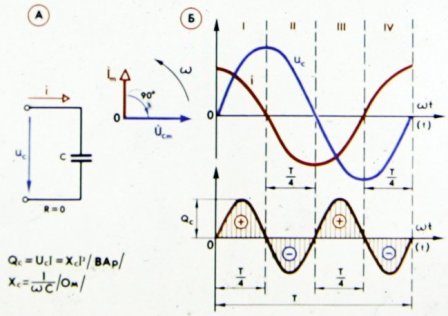
I fig. 3 visar kurvorna som kännetecknar fasförhållandet mellan ström och spänning i en krets innehållande kapacitiv och aktiv resistans.

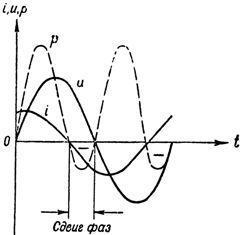
Ris. 3. Ström, spänning och effekt i en krets med en kondensator och ett aktivt motstånd

Som framgår av figuren ökar strömmen i detta fall spänningen inte med en fjärdedel av en period, utan med mindre, eftersom det aktiva motståndet bryter mot kretsens rent kapacitiva (reaktiva) natur, vilket framgår av den reducerade fasen flytta. Nu definieras spänningen vid kretsterminalerna som summan av två komponenter: den reaktiva komponenten av spänningen kommer att övervinna kretsens kapacitiva resistans och den aktiva komponenten av spänningen och övervinna dess aktiva motstånd.

Ju större kretsens aktiva resistans är, desto mindre fasförskjutning mellan ström och spänning.

Kurvan för effektändringen i kretsen (se fig. 3) fick två gånger under perioden ett negativt tecken, vilket, som vi redan vet, är en följd av kretsens reaktiva karaktär. Ju mindre reaktiv kretsen är, desto mindre fasförskjutning mellan ström och spänning, och desto mer strömkälla förbrukar den kretsen.

Läs också: Spänningsresonans