Vad är en elförsörjning?

Den moderna människan möter ständigt elektricitet i vardagen och på jobbet, använder enheter som förbrukar elektrisk ström och enheter som genererar den. När du arbetar med dem bör du alltid ta hänsyn till deras kapacitet som är inneboende i de tekniska egenskaperna.

En av huvudindikatorerna för alla elektriska enheter är en sådan fysisk mängd som elektrisk energi... Det är vanligt att kalla intensiteten eller hastigheten för generering, överföring eller omvandling av elektricitet till andra typer av energi, till exempel värme, ljus, mekanisk.

Transport eller överföring av stor elektrisk energi för industriella ändamål utförs enligt högspänningsledningar.

Omvandling elektrisk energi utförs vid transformatorstationer.

Elförbrukning förekommer i hushålls- och industriapparater för olika ändamål. En av deras vanliga typer är glödlampor av olika klasser.

Den elektriska effekten hos generatorer, kraftledningar och förbrukare i DC- och AC-kretsar har samma fysiska betydelse, som samtidigt uttrycks i olika förhållanden beroende på formen på de sammansatta signalerna. För att definiera de allmänna mönstren, föreställningar om momentana värden... De betonar återigen beroendet av omvandlingshastigheten för elektricitet i tid.

Bestämning av momentan elektrisk effekt

Inom teoretisk elektroteknik används för att härleda de grundläggande sambanden mellan ström, spänning och effekt deras bilder i form av momentana värden, som är fixerade vid en viss tidpunkt.

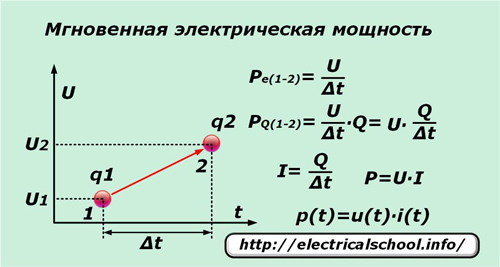
Om under en mycket kort tidsperiod ∆t en enda elementär laddning q under påverkan av spänningen U flyttar sig från punkt «1» till punkt «2», utför den arbete lika med potentialskillnaden mellan dessa punkter. Om vi ​​dividerar det med tidsintervallet ∆t får vi uttrycket för den momentana effekten per laddningsenhet Pe (1-2).

Eftersom inte bara den enda laddningen rör sig under verkan av den applicerade spänningen, utan också alla de intilliggande som är under påverkan av denna kraft, vars antal lämpligen representeras av talet Q, då det momentana värdet av effekten PQ (1-2) kan skrivas för dem.

Efter att ha utfört enkla transformationer får vi uttrycket för effekten P och beroendet av dess momentana värde p (t) på komponenterna i produkten av den momentana strömmen i (t) och spänningen u (t).

Bestämning av konstant elektrisk effekt

V DC-kretsar storleken på spänningsfallet i kretssektionen och strömmen som flyter genom den ändras inte och förblir stabil, lika med de momentana värdena.Därför kan effekten i denna krets bestämmas genom att multiplicera dessa värden eller dividera det perfekta arbetet A med tiden för dess utförande, som visas i den förklarande bilden.

Bestämning av elektrisk växelströmseffekt

Lagarna för sinusformad variation av strömmar och spänningar som sänds genom elektriska nätverk tvingar deras inflytande på kraftuttrycket i sådana kretsar. Här spelar skenbar kraft in, som beskrivs av effekttriangeln och består av aktiva och reaktiva komponenter.

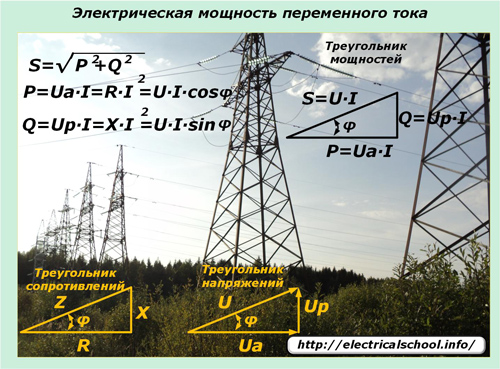
En sinusformad elektrisk ström när den passerar genom kraftledningar med blandade typer av belastningar i alla sektioner ändrar inte formen på dess överton, och spänningsfallet vid reaktiva belastningar skiftar i fas i en viss riktning. Momentvärdeuttryck hjälper till att förstå effekten av applicerade belastningar på effektändringen i kretsen och dess riktning.

Var samtidigt omedelbart uppmärksam på det faktum att riktningen för strömflödet från generatorn till konsumenten och den överförda effekten genom den skapade kretsen är helt olika saker, som i vissa fall inte bara kan sammanfalla, utan också vara riktade i motsatta riktningar.

Betrakta dessa relationer i deras ideala, rena manifestation för olika typer av laster:

• aktiva;

• kapacitiv;

• induktiv.

Aktiv lasteffektförlust

Vi kommer att anta att generatorn producerar en ideal sinusformad spänning u som appliceras på kretsens rent aktiva motstånd. Amperemeter A och voltmeter V mäter ström I och spänning U varje gång t.

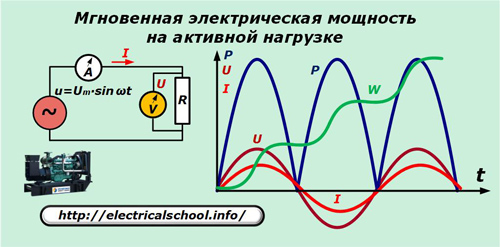
Grafen visar att sinusformerna för strömmen och spänningsfallet över det aktiva motståndet matchar i frekvens och fas, vilket ger samma svängningar. Kraften som uttrycks av deras produkt oscillerar med två gånger frekvensen och förblir alltid positiv.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Om vi ​​går till uttrycket Driftspänning, då får vi: p = P ∙ (1-cos2ωt).

Vi kommer då att integrera effekten över perioden för en svängning T och vi kommer att kunna märka att energiförstärkningen ∆W under detta intervall ökar. Med tiden fortsätter motståndet att förbruka nya delar av elektriciteten, som visas i grafen.

Med reaktiva belastningar är egenskaperna hos energiförbrukningen olika, de har en annan form.

Kapacitiv effektförlust

I generatorns elektriska krets, byt ut det resistiva elementet med en kondensator med kapacitans C.

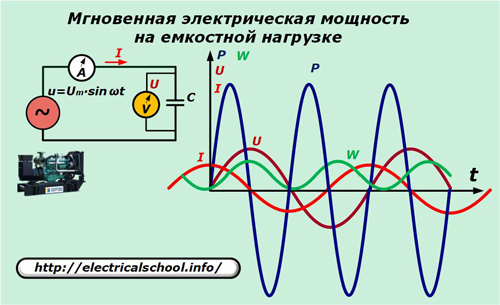
Förhållandet mellan strömmen och spänningsfallet i kapacitansen uttrycks av förhållandet: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Vi multiplicerar värdena för de momentana uttrycken av ström med spänning och får värdet på den effekt som förbrukas av den kapacitiva belastningen.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt sin = U2/ (2X.

Här kan du se att effekten fluktuerar runt noll vid dubbla frekvensen av den pålagda spänningen. Dess totala värde för den harmoniska perioden, såväl som energiförstärkningen, är noll.

Detta innebär att energi rör sig längs den slutna kretsen i kretsen i båda riktningarna, men inte fungerar.Ett sådant faktum förklaras av det faktum att när källspänningen ökar i absolut värde, är effekten positiv, och energiflödet genom kretsen riktas till behållaren, där energi ackumuleras.

Efter att spänningen passerat till den fallande övertonssektionen återförs energi från kondensatorn till kretsen till källan. Inget användbart arbete görs i någon av processerna.

Effektförlust i en induktiv last

Nu, i matningskretsen, byt ut kondensatorn med induktans L.

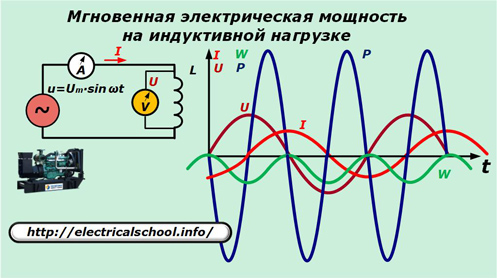
Här uttrycks strömmen genom induktansen med förhållandet:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Då får vi

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sinω2ωt (2ХL) ∙Sin -U2ωt (2).

De resulterande uttrycken tillåter oss att se karaktären av förändringen i kraftens riktning och ökningen av energi på induktansen, som utför samma svängningar som är värdelösa för att utföra arbete, som på kapacitansen.

Effekten som frigörs i reaktiva belastningar kallas reaktiv komponent. Under ideala förhållanden, när anslutningstrådarna inte har något aktivt motstånd, verkar det ofarligt och orsakar ingen skada. Men under verkliga effektförhållanden orsakar periodiska transienter och reaktiva effektfluktuationer uppvärmning av alla aktiva element, inklusive anslutningskablar, för vilka en del energi förbrukas och värdet på den applicerade fulla effekten av källan minskar.

Huvudskillnaden mellan den reaktiva komponenten av kraft är att den inte utför användbart arbete alls, men leder till förluster av elektrisk energi och överbelastning på utrustning, vilket är särskilt farligt i kritiska situationer.

Av dessa skäl, för att eliminera påverkan av reaktiv effekt, t.ex tekniska system för dess ersättning.

Effektfördelning vid blandad belastning

Som ett exempel använder vi belastningen av en generator med en aktiv kapacitiv karaktäristik.

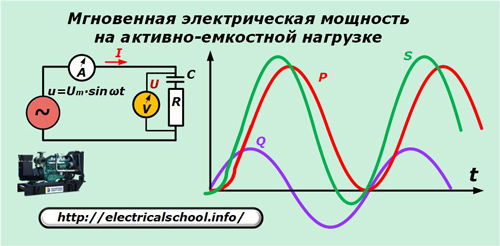
För att förenkla bilden visas inte sinusoiderna för strömmar och spänningar i den givna grafen, men man bör komma ihåg att med en aktiv-kapacitiv karaktär av belastningen leder strömvektorn spänningen.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Efter transformationer får vi: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Dessa två termer i det sista uttrycket är de aktiva och reaktiva komponenterna av den momentana skenbara kraften. Endast den första av dessa fungerar bra.

Verktyg för effektmätning

För att analysera förbrukningen av el och beräkna för den används mätanordningar, som länge har kallats "Räknare"… Deras arbete är baserat på att mäta de effektiva värdena för ström och spänning och automatiskt multiplicera dem med en utmatning av information.

Mätare visar energiförbrukningen genom att räkna drifttiden för elektriska apparater på en inkrementell basis från det ögonblick som mätaren slås på under belastning.

För att mäta den aktiva komponenten av effekt i AC-kretsar, wattmätare, och reaktiva - varmare. De har olika enhetsbeteckningar:

• watt (W, W);

• var (var, var, var).

För att bestämma den totala energiförbrukningen är det nödvändigt att beräkna dess värde med hjälp av effekttriangelformeln baserat på avläsningarna av wattmätaren och varmetern. Det uttrycks i sina egna enheter - volt-ampere.

De accepterade beteckningarna för varje enheter hjälper elektriker att bedöma inte bara dess värde utan också kraftkomponentens natur.