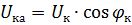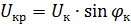Transformator kortslutningsläge

Transformatorns kortslutningsläge är ett sådant läge när terminalerna på sekundärlindningen är stängda av en strömledare med ett motstånd lika med noll (ZH = 0). En kortslutning av transformatorn under drift skapar ett nödläge, eftersom sekundärströmmen, och därför primärströmmen, ökar flera tiotals gånger jämfört med den nominella. I kretsar med transformatorer tillhandahålls därför ett skydd som automatiskt stänger av transformatorn vid kortslutning.

Under laboratorieförhållanden är det möjligt att utföra en testkortslutning av transformatorn, där terminalerna på sekundärlindningen kortsluts, och en spänning Uk appliceras på primärlindningen, där strömmen i primärlindningen gör inte överstiga det nominella värdet (Ik < I1nom). I detta fall betecknas spänningen Uk, uttryckt i procent, med Ik = I1nom, med uK och kallas transformatorns kortslutningsspänning. Det egenskap hos transformatornanges i passet.

Således (%):

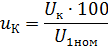
där U1nom är den nominella primärspänningen.

Kortslutningsspänningen beror på transformatorlindningarnas högre spänning. Till exempel, vid en högre spänning på 6-10 kV uK = 5,5 %, vid 35 kV uK = 6,5 ÷ 7,5 %, vid 110 kV uK = 10,5 %, etc. Som du kan se, när märkspänningen ökar, ökar kortslutningsspänningen hos transformatorn.

När spänningen Uc är 5-10 % av den märkta primärspänningen, minskar magnetiseringsströmmen (obelastningsström) 10-20 gånger eller till och med mer markant. Därför anses det i kortslutningsläge

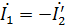
Det magnetiska huvudflödet F minskar också med en faktor 10–20, och lindningarnas läckströmmar blir proportionerliga med huvudflödet.

Eftersom när transformatorns sekundärlindning är kortsluten är spänningen vid dess terminaler U2 = 0, t.ex. etc. s. eftersom det tar formen

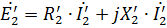
och spänningsekvationen för transformatorn skrivs som

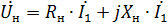
Denna ekvation motsvarar transformatorns ekvivalentkrets som visas i fig. 1.

Vektordiagrammet för kortslutningstransformatorn som motsvarar ekvationen och diagrammet i fig. 1 visas i FIG. 2. Kortslutningsspänning har aktiva och reaktiva komponenter. Vinkeln φk mellan vektorerna för dessa spänningar och strömmar beror på förhållandet mellan de aktiva och reaktiva induktiva komponenterna i transformatormotståndet.

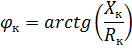
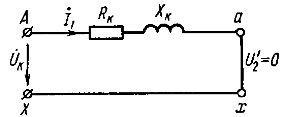
Ris. 1. Motsvarande krets för transformatorn vid kortslutning

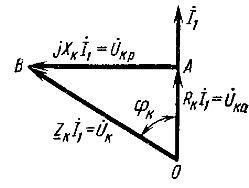
Ris. 2. Vektordiagram över transformatorn under kortslutning

För transformatorer med märkeffekt 5-50 kVA XK / RK = 1 ÷ 2; med märkeffekt 6300 kVA eller mer XK / RK = 10 eller mer. Därför tror man att för högeffekttransformatorer UK = Ucr och impedansen ZK = Xk.

Kortslutningsupplevelse.

Detta experiment, liksom tomgångsexperimentet, utförs för att bestämma transformatorns parametrar. En krets är sammansatt (fig. 3) i vilken sekundärlindningen kortsluts av en metallbygel eller tråd med ett motstånd nära noll. En spänning Uk appliceras på primärlindningen, vid vilken strömmen i den är lika med det nominella värdet I1nom.

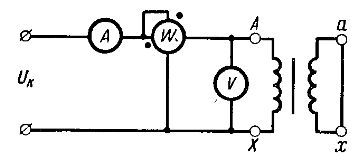
Ris. 3. Schematisk beskrivning av transformatorns kortslutningsexperiment

Enligt mätdata bestäms följande parametrar för transformatorn.

Kortslutningsspänning

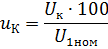
där UK är spänningen mätt med en voltmeter vid I1, = I1nom I kortslutningsläge är UK mycket liten, så tomgångsförlusterna är hundratals gånger mindre än vid nominell spänning. Således kan vi anta att Ppo = 0 och effekten som mäts av wattmätaren är effektförlusten Ppk, på grund av transformatorlindningarnas aktiva motstånd.

Vid ström I1, = I1nom få nominella effektförluster för uppvärmning av lindningarna Rpk.nom, som kallas elektriska förluster eller kortslutningsförluster.

Från spänningsekvationen för transformatorn, såväl som från den ekvivalenta kretsen (se fig. 1), får vi

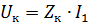
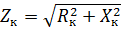
där ZK är transformatorns impedans.

Genom att mäta Uk och I1 kan du beräkna transformatorimpedansen

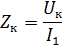
Effektförlusten under en kortslutning kan uttryckas med formeln

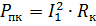
Därav aktivt motstånd hos transformatorlindningarna

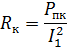
hittas från wattmätaren och amperemetern. Genom att känna till Zk och RK kan du beräkna lindningarnas induktiva motstånd:

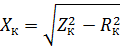
Genom att känna till transformatorns Zk, RK och Xk kan du bygga kortslutningsspänningarna för huvuddeltatet (triangel OAB i fig. 2) och även bestämma de aktiva och induktiva komponenterna i kortslutningsspänningen: