Bestämning av motoreffekt under upprepad transient drift

Driftssättet för den elektriska drivenheten, i vilken driftsperioderna är av sådan varaktighet, och så växlar med pauser av en viss varaktighet, att temperaturen på alla enheter som utgör den elektriska drivenheten inte når ett stabilt värde, varken under varje arbetsperiod, eller under varje rast, kallas avbrott.

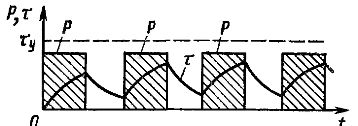
Den periodiska belastningsregimen motsvarar grafer som liknar de som visas i fig. 1. Överhettningen av elmotorn varierar längs den streckade linjen på en såg som består av alternerande segment av värme- och kylkurvor. Intermittent belastningsläge är typiskt för de flesta verktygsmaskiner.

Ris. 1. Intermittent belastningsschema

Effekten hos en elektrisk motor som arbetar i periodiskt läge bestäms lämpligast av formeln för genomsnittliga förluster, som kan skrivas som

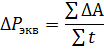
där ΔA är energiförlusten vid varje belastningsvärde, inklusive start- och stoppprocesser.

När elmotorn inte fungerar försämras kylförhållandena avsevärt. Detta beaktas genom att introducera experimentella koefficienter β0 <1. Paustiden t0 multipliceras med koefficienten β0, som ett resultat av vilket nämnaren i formeln minskar, och de ekvivalenta förlusterna ΔREKV ökar och följaktligen ökar den nominella effekten hos den elektriska motorn.

För asynkronskyddade motorer i A-serien med en synkron hastighet på 1500 rpm och en effekt på 1-100 kW är β0-koefficienten 0,50-0,17, och för nedblåsningsmotorer β0 = 0,45-0,3 (med en ökning av Пн , koefficienten β0 minskar). För stängda motorer är β0 nära enhet (0,93-0,98). Detta beror på att ventilationseffektiviteten hos stängda motorer är låg.

Vid start och stopp är elmotorns medelhastighet lägre än den nominella, vilket resulterar i att kylningen av elmotorn också försämras, vilket kännetecknas av koefficienten

Vid bestämning av koefficienten β1 antas villkorligt att förändringen i rotationsfrekvensen sker enligt en linjär lag och att koefficienten β1 är linjärt beroende av den.

Genom att känna till koefficienterna β0 och β1 får vi

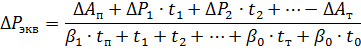
där ΔР1, ΔР2, — effektförluster vid olika belastningar, kW; t1 t2 — verkanstid för dessa laster, s; tn, tT, t0 — start-, fördröjnings- och paustid, s; ΔАп ΔАТ — energiförluster i motorn under start och stopp, kJ.

Som nämnts ovan måste varje motor väljas för uppvärmning och överbelastning. För att tillämpa metoden för genomsnittliga förluster är det nödvändigt att ställa in en viss elmotor i förväg, som i detta fall också rekommenderas att väljas enligt överbelastningsförhållandena.Den ekvivalenta effektformeln kan användas för en grov beräkning i fall där start och stopp är sällsynta och inte nämnvärt påverkar uppvärmningen av elmotorn.

Inom maskinteknik, för drift i intermittent belastningsläge, används elmotorer konstruerade för att arbeta med en kontinuerlig belastning. Elindustrin tillverkar även motorer speciellt utformade för att hantera intermittenta belastningar, som används i stor utsträckning i lyft- och transportkonstruktioner. Sådana elmotorer väljs med hänsyn till den relativa varaktigheten av inkluderingen:

där tp är motorns gångtid; t0 — pauslängd.

Ett exempel på att välja en motor med effekt i flera korttidsdriftsläge.

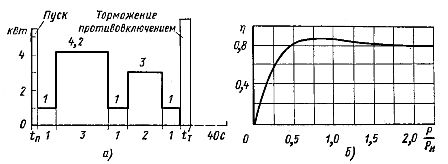
Bestäm elmotorns effekt vid n0 - 1500 rpm; motorn arbetar enligt belastningsschemat som visas i fig. 2, a. Elmotorns axeleffekt vid tomgång Pxx = 1 kW. Maskinens reducerade tröghetsmoment Jc = 0,045 kg-m2.

Svar:

1. Förvälj elmotorn enligt överbelastningsförhållandena, såsom λ = 1,6:

Enligt katalogen väljer vi en elmotor med den skyddade versionen av närmaste höga effekt (2,8 kW), där mån = 1420 rpm;

För denna motor λ = 0,85 • 2 = 1,7. På så sätt väljs motorn med en viss överbelastningsgräns.

Beroendet η = f (P / Pн) för denna motor visas i fig. 2, b.

Ris. 2. Beroenden N = f (t) och η = f (P / Pн)

2. Enligt formeln

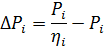
vi upptäcker förluster vid potens 1; 3; 4,2 kW (enligt schema). Förlusterna är respektive 0,35; 0,65 och 1 kW. Vi finner förluster vid Pn = 2,8 kW, vilket är ΔPn = 0,57 kW.

3. Bestäm starttiden och stopptiden genom motstånd:

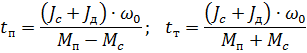
var:

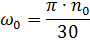
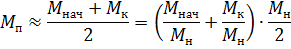
Vi får tn = 0,30 s; tt = 0,21 s.

4. Bestäm start- och stoppförlusterna:

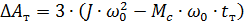
Vi får ΔAp = 1,8 kJ och ΔAt = 3,8 kJ.

5. Hitta motsvarande förluster i slingan:

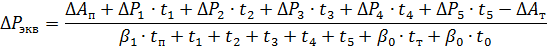
var

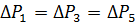
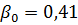
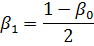
Vi får ΔREKV = 0,44 kW. Eftersom ΔPn = 0,57 är ΔREKV <ΔPn och därför motorn korrekt vald.