Lagen om bevarande av energi

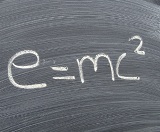Modern fysik känner till många typer av energi som är förknippade med rörelse eller olika inbördes arrangemang av en mängd olika materialkroppar eller partiklar, till exempel har varje rörlig kropp kinetisk energi som är proportionell mot kvadraten på dess hastighet. Denna energi kan förändras om kroppens hastighet ökar eller minskar. En kropp som höjs över marken har en gravitationspotential energi som varierar tre förändringar i kroppens höjd.

Stationära elektriska laddningar som ligger en bit från varandra har en elektrostatisk potentiell energi i enlighet med att laddningarna enligt Coulombs lag antingen attraherar (om de har olika tecken) eller stöter bort med en kraft som är omvänt proportionell mot kvadraten på avståndet mellan dem.

Kinetisk och potentiell energi innehas av molekyler, atomer och partiklar, deras beståndsdelar - elektroner, protoner, neutroner, etc. i form av mekaniskt arbete, i flödet av elektrisk ström, i överföringen av värme, i förändringen av kropparnas inre tillstånd, i utbredningen av elektromagnetiska vågor, etc.

För mer än 100 år sedan etablerades en grundläggande fysiklag, enligt vilken energi inte kan försvinna eller uppstå ur ingenting. Hon kan bara byta från en typ till en annan... Denna lag kallas lagen om energibevarande.

I verk av A. Einstein är denna lag avsevärt utvecklad. Einstein etablerade utbytbarheten mellan energi och massa och utökade därigenom tolkningen av lagen om energibevarande, som numera vanligen anges som lagen om bevarande av energi och massa.

I enlighet med Einsteins teori är varje förändring i kroppens energi dE relaterad till en förändring av dess massa dm med formeln dE =dmc2, där c är ljusets hastighet i ett vakuum lika med 3 x 108 Miss.

Av denna formel, i synnerhet, följer det att om, som ett resultat av någon process, massan av alla kroppar som är involverade i processen minskar med 1 g, då energin är lika med 9×1013 J, vilket motsvarar 3000 ton av standardbränsle.

Dessa förhållanden är av primär betydelse i analysen av kärnomvandlingar. I de flesta makroskopiska processer kan förändringen i massa försummas och endast lagen om energibevarande kan talas om.

Låt oss spåra omvandlingarna av energi på något konkret exempel. Betrakta hela kedjan av energiomvandlingar som krävs för att producera någon del på en svarv (Fig. 1). Låt den initiala energin 1, vars mängd vi tar som 100%, erhålls på grund av fullständig förbränning av en viss mängd fossilt bränsle. Därför, för vårt exempel, finns 100% av den initiala energin i produkterna från bränsleförbränning, som har en hög (cirka 2000 K) temperatur.

Förbränningsprodukterna i kraftverkets panna, när de kyls, ger upp sin inre energi i form av värme till vatten och vattenånga. Av tekniska och ekonomiska skäl kan dock förbränningsprodukterna inte kylas till omgivningstemperatur. De kastas ut genom röret till atmosfären vid en temperatur på cirka 400 K och tar med sig en del av den ursprungliga energin. Därför kommer endast 95 % av den initiala energin att överföras till vattenångans inre energi.

Den resulterande vattenångan kommer in i ångturbinen, där dess inre energi initialt delvis omvandlas till kinetisk energi hos ångsträngarna, som sedan kommer att överföras som mekanisk energi till turbinrotorn.

Endast en del av ångenergin kan omvandlas till mekanisk energi. Resten ges till kylvattnet när ånga kondenseras i kondensorn. I vårt exempel antog vi att energin som överförs till turbinrotorn skulle vara cirka 38 %, vilket ungefär motsvarar tillståndet i moderna kraftverk.

Vid omvandling av mekanisk energi till elektrisk energi på grund av den sk Jouleförluster i generatorns rotor- och statorlindningar kommer att förlora cirka 2 % av energin. Som ett resultat kommer cirka 36 % av den initiala energin att gå in i nätet.

En elmotor omvandlar endast en del av den elektriska energin som tillförs den till mekanisk energi för att rotera svarven. I vårt exempel kommer cirka 9 % av energin i form av Joule-värme i motorlindningarna och friktionsvärme i dess lager att släppas ut i den omgivande atmosfären.

Således kommer endast 27% av den initiala energin att levereras till maskinens arbetsorgan. Men energimissöden slutar inte heller där. Det visar sig att det mesta av energin under bearbetningen av en detalj går åt till friktion och i form av värme tas bort med vätskan som kyler delen. Teoretiskt sett skulle endast en mycket liten del (i vårt exempel antas 2%) av den initiala energin vara tillräcklig för att erhålla den önskade delen av den ursprungliga delen.

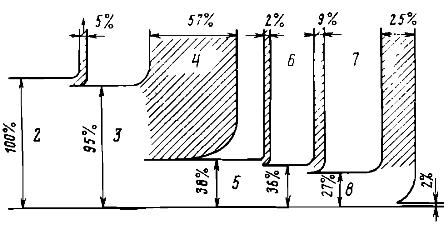
Ris. 1. Diagram över energiomvandlingar under bearbetning av ett arbetsstycke på en svarv: 1 — energiförlust med avgaser, 2 — förbränningsprodukters inre energi, 3 — arbetsvätskans inre energi — vattenånga, 4 — värme som frigörs från kylningen vatten i en turbinkondensor, 5 — mekanisk energi hos rotorn på en turbingenerator, 6 — förluster i den elektriska generatorn, 7 — spill i maskinens elektriska drivning, 8 — mekanisk rotationsenergi för maskinen, 9 — friktionsenergi arbete, som omvandlas till värme, separerat från vätskan, kyldelen, 10 — ökar den inre energin hos delen och flisen efter bearbetning ...

Åtminstone tre mycket användbara slutsatser kan dras från exemplet i fråga, om det anses vara ganska typiskt.

För det första, vid varje steg av energiomvandlingen går en del av det förlorat... Detta uttalande ska inte förstås som ett brott mot lagen om bevarande av energi. Det går förlorat på grund av den användbara effekten för vilken motsvarande transformation utförs. Den totala mängden energi efter omvandlingen förblir oförändrad.

Om processen för energiomvandling och överföring sker i en viss maskin eller apparat, kännetecknas denna enhets effektivitet vanligtvis av effektivitet (effektivitet)... Ett diagram över en sådan enhet visas i fig. 2.

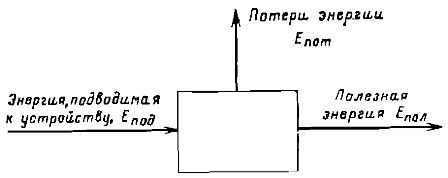
Ris. 2. Schema för att bestämma effektiviteten hos en enhet som omvandlar energi.

Med hjälp av notationen som visas i figuren kan effektiviteten definieras som Effektivitet = Epol/Epod

Det är tydligt att i det här fallet, baserat på lagen om energibevarande, måste det finnas Epod = Epol + Epot

Därför kan effektiviteten också skrivas på följande sätt: effektivitet = 1 — (Epot / Epol)

För att återgå till exemplet som visas i FIG. 1, kan vi säga att pannans verkningsgrad är 95%, effektiviteten för att omvandla den interna energin av ånga till mekaniskt arbete är 40%, effektiviteten hos den elektriska generatorn är 95%, verkningsgraden är - den elektriska drivningen av en maskin — 75%, och effektiviteten för den faktiska bearbetningen av arbetsstycket är cirka 7%.

Tidigare, när lagarna för energiomvandling ännu inte var kända, var människors dröm att skapa en så kallad evighetsmaskin - en anordning som skulle göra användbart arbete utan att spendera energi. En sådan hypotetisk motor, vars existens skulle bryta mot lagen om energibevarande, kallas idag en evighetsmaskin av det första slaget, till skillnad från en evighetsmaskin av det andra slaget. Idag är det naturligtvis ingen som tar seriöst möjligheten att skapa en evighetsmaskin av det första slaget.

För det andra omvandlas alla energiförluster i slutändan till värme, som frigörs antingen till atmosfärisk luft eller till vatten från naturliga reservoarer.

För det tredje använder människor bara en liten del av den primära energin som förbrukas för att få den relevanta gynnsamma effekten.

Detta är särskilt tydligt när man tittar på energitransportkostnader. I idealiserad mekanik, som inte tar hänsyn till friktionskrafter, kräver rörliga laster i horisontalplanet ingen energi.

Under verkliga förhållanden används all energi som förbrukas av ett fordon för att övervinna friktionskrafter och luftmotståndskrafter, det vill säga i slutändan omvandlas all energi som förbrukas vid transport till värme. I detta avseende är följande siffror intressanta, som kännetecknar arbetet med att flytta 1 ton last på ett avstånd av 1 km med olika typer av transporter: flygplan — 7,6 kWh / (t-km), bil — 0,51 kWh / ( t- km), tåg-0,12 kWh / (t-km).

Därmed kan samma fördelaktiga effekt uppnås med flygtransporter på bekostnad av 60 gånger större energiförbrukning än med järnväg. Hög energiförbrukning ger förstås betydande tidsbesparingar, men även vid samma hastighet (bil och tåg) skiljer sig energikostnaderna med 4 gånger.

Det här exemplet tyder på att människor ofta gör avvägningar med energieffektivitet för att uppnå andra mål, till exempel komfort, hastighet etc. Energieffektiviteten i själva processen är som regel av lite intresse för oss — den allmänna tekniska och ekonomiska utvärderingar av processernas effektivitet är viktigt... Men i takt med att priset på primärenergikomponenter ökar blir energikomponenten i tekniska och ekonomiska utvärderingar allt viktigare.