Transformatordriftlägen

Beroende på lastens värde kan transformatorn arbeta i tre lägen:

1. Tomgångsdrift vid belastningsmotstånd zn = ∞.

2. Kortslutning vid zn = 0.

3. Laddningsläge vid 0 <zn <∞.

Med parametrarna för den ekvivalenta kretsen kan du analysera vilket driftsätt som helst för transformatorn... Parametrarna själva bestäms baserat på tomgångs- och kortslutningsexperiment. Vid tomgång är transformatorns sekundärlindning öppen.

Ett tomgångstransformatortest utförs för att bestämma transformationsförhållandet, effektförlusterna i stålet och parametrarna för magnetiseringsgrenen av den ekvivalenta kretsen, vanligtvis utförd vid primärlindningens märkspänning.

För enfas transformator baserat på data från tomgångstestet är det möjligt att beräkna:

— omvandlingsfaktor

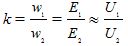
— procentandel av tomgångsström

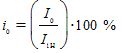
Bestäms det aktiva motståndet för grenmagnetiseringen r0 av tillståndet

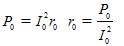
— total resistans hos magnetiseringsgrenen

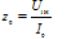
— magnetiseringsgrenens induktiva resistans

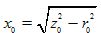
Tomgångseffektfaktorn definieras också ofta som:

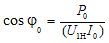
I vissa fall utförs tomgångstestet för flera värden på primärlindningsspänningen: från U1 ≈ 0,3U1n till U1 ≈ 1,1U1n. Baserat på erhållna data ritas tomgångskarakteristika, vilka är beroendet av PO, z0, r0 och cosφ som en funktion av spänningen Ul. Med hjälp av tomgångsegenskaperna är det möjligt att ställa in värdena för de specificerade kvantiteterna till vilket värde som helst på spänningen U1.

För att bestämma kortslutningsspänningen testas förlusterna i lindningarna och resistanserna rk och xk i en kortslutning. I detta fall appliceras en sådan reducerad spänning på primärlindningen så att strömmarna i de kortslutna transformatorlindningarna är lika med deras nominella värden, dvs. I1k = I1n, I2k = I2n. Primärlindningens spänning, vid vilken de specificerade villkoren är uppfyllda, kallas den nominella kortslutningsspänningen Ukn.

Med tanke på att Ucn vanligtvis bara är 5-10 % av U1n, är det ömsesidiga induktionsflödet för transformatorkärnan under kortslutningstestet tiotals gånger mindre än i det nominella läget, och transformatorstålet är omättat. Därför försummas förlusterna i stålet och det anses att all effekt Pcn som tillförs primärlindningen går åt till att värma lindningarna och bestämmer värdet på det aktiva kortslutningsmotståndet rc.

Under experimentet mäts spänningen Ukn, strömmen I1k = I1n och effekten Pkn för primärspolen. Baserat på dessa data kan du bestämma:

— procentandel av kortslutningsspänningen

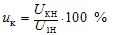
— aktivt kortslutningsmotstånd

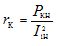
— Aktiva resistanser hos primär- och reducerade sekundärlindningar, ungefär lika med halva kortslutningsresistansen

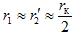
— kortslutningsimpedans

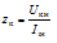
— kortslutningsinduktivt motstånd

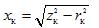
— induktivt motstånd för primärlindningen och den reducerade sekundärlindningen, ungefär lika med hälften av det kortslutningsinduktiva motståndet

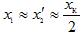
— resistans för sekundärlindningen på en riktig transformator:

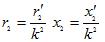
— induktiv, aktiv och total procentuell kortslutningsspänning:

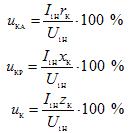
V belastningsläge är det mycket viktigt att veta hur belastningsparametrarna påverkar effektiviteten och spänningsvariationen vid sekundärlindningens terminaler.

Transformatoreffektivitet är förhållandet mellan aktiv effekt som levereras till lasten och aktiv effekt som tillförs transformatorn.

Transformatorns effektivitet är av stor betydelse. För krafttransformatorer med låg effekt är det cirka 0,95, och för transformatorer med en kapacitet på flera tiotusentals kilovolt-ampere når det 0,995.

Att bestämma effektiviteten med formeln med hjälp av direkt uppmätta potenser P1 och P2 ger ett stort fel. Det är bekvämare att presentera denna formel i en annan form:

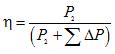
var är summan av förlusterna i transformatorn.

Det finns två typer av förluster i en transformator: magnetiska förluster orsakade av passage av magnetiskt flöde genom den magnetiska kretsen och elektriska förluster till följd av strömflödet genom lindningarna.

Eftersom transformatorns magnetiska flöde vid U1 = const och förändringen av sekundärströmmen från noll till nominell praktiskt taget förblir konstant, kan de magnetiska förlusterna i detta belastningsområde också antas vara konstanta och lika med tomgångsförlusterna.

De elektriska förlusterna i lindningarnas koppar ∆Pm är proportionella mot strömmens kvadrat. Det är bekvämt att uttrycka dem som kortslutningsförluster Pcn som erhålls vid märkström,

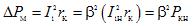
där β är belastningsfaktorn,

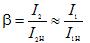
Beräkningsformler för att bestämma transformatorns effektivitet:

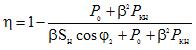
där Sn är transformatorns nominella skenbara effekt; φ2 är fasvinkeln mellan spänningen och strömmen i lasten.

Den maximala effektiviteten kan hittas genom att likställa den första derivatan med noll. I det här fallet finner vi att verkningsgraden har maximala värden vid en sådan belastning när de konstanta (strömoberoende) förlusterna P0 är lika med de alternerande (strömberoende) förlusterna, varav

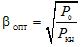
För moderna kraftoljetransformatorer βopt = 0,5 — 0,7. Med en sådan belastning fungerar transformatorn oftast under drift.

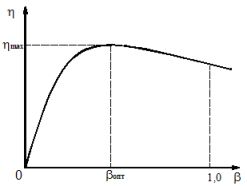
Grafen över beroendet η = f (β) visas i figur 1.

Figur 1. Kurva för förändringen i transformatorverkningsgrad beroende på belastningsfaktor

För att bestämma den procentuella förändringen i sekundärspänningen för en enfastransformator, använd ekvationen

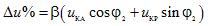
där uKA och uKR är de aktiva och reaktiva komponenterna i kortslutningsspänningen, uttryckt i procent.

Förändringen i transformatorspänningen beror på belastningsfaktorn (β), dess natur (vinkel φ2) och komponenterna i kortslutningsspänningen (uKA och uKR).

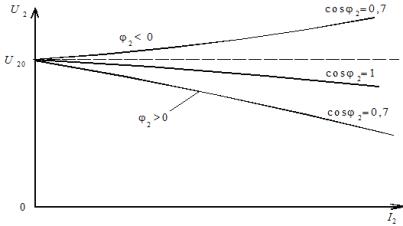
Externa egenskaper hos transformatorn är beroendet vid U1 = const och cosφ2 = const (Figur 2).

Figur 2. Yttre egenskaper hos mellan- och högeffekttransformatorer för olika typer av belastning