Asynkron motordrift

Driften av induktionsmotorn uttrycks grafiskt beroende av hastighet n2, verkningsgrad η, användbart vridmoment (axelvridmoment) M2, effektfaktor cos φ och statorström I1 på användbar effekt P2 vid U1 = const f1 = konst.

Hastighetskarakteristik n2 = f (P2). Induktionsmotorns rotorhastighet n2 = n1 (1 — s).

Slide s = Pe2 / Rem, dvs. induktionsmotorns slirning och därför dess hastighet bestäms av förhållandet mellan elektriska förluster i rotorn och elektromagnetisk effekt. Om man bortser från elektriska förluster i rotorn vid tomgång kan vi ta Pe2 = 0 och därför s ≈ 0 och n20 ≈ n1.

När axelbelastningen ökar asynkron motor förhållandet s = Pe2 / Pem ökar och når värden på 0,01 - 0,08 vid nominell belastning. Följaktligen är beroendet n2 = f (P2) en kurva som lutar något mot abskissaxeln. Men när motorrotorns aktiva motstånd r2' ökar, ökar lutningen på denna kurva. I detta fall ökar förändringar i frekvensen för induktionsmotorn n2 med fluktuationer i belastningen P2.Detta förklaras av det faktum att när r2' ökar, ökar de elektriska förlusterna i rotorn.

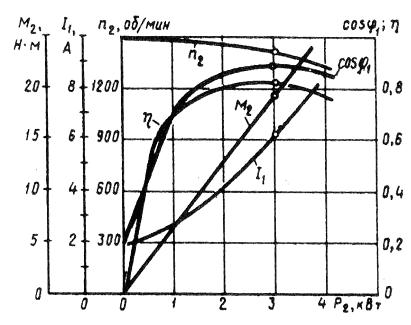
Ris. 1. Egenskaper för driften av induktionsmotorn

Beroende M2 ​​= f (P2). Beroendet av det användbara vridmomentet från asynkronmotorns M2 axel på nyttoeffekten P2 bestäms av uttrycket M2 = P2 / ω2 = 60 P2 / (2πn2) = 9,55P2 / n2,

där P2 — användbar effekt, W; ω2 = 2πf 2/60 är rotorns vinkelfrekvens.

Det följer av detta uttryck att om n2 = const, så är grafen M2 = f2 (P2) en rät linje. Men i en induktionsmotor med en ökning av belastningen P2 minskar rotorns hastighet och därför ökar det användbara momentet för axeln M2 med en ökning av belastningen lite snabbare än belastningen och därför ökar grafen M2 = f (P2) ) har en krökt form.

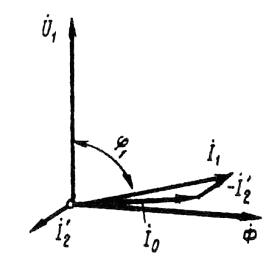Ris. 2. Vektordiagram över en induktionsmotor vid låg belastning

Beroende cos φ1 = f (P2). På grund av det faktum att induktionsmotorns I1 statorström har en reaktiv (induktiv) komponent som är nödvändig för att skapa ett magnetfält i statorn, är effektfaktorn för induktionsmotorer mindre än enhet. Det lägsta värdet på effektfaktorn motsvarar tomgång. Detta förklaras av det faktum att tomgångsströmmen för elmotorn I0 vid vilken belastning som helst förblir praktiskt taget oförändrad. Därför, vid låga motorbelastningar, är statorströmmen liten och i stort sett reaktiv (I1 ≈ I0). Som ett resultat är fasförskjutningen av statorströmmen med avseende på spänningen signifikant (φ1 ≈ φ0), endast något mindre än 90° (fig. 2).

Effektfaktorn utan belastning för induktionsmotorer är vanligtvis mindre än 0,2.När belastningen på motoraxeln ökar, ökar den aktiva komponenten av strömmen I1 och effektfaktorn ökar och når det högsta värdet (0,80 - 0,90) vid en belastning nära den nominella. En ytterligare ökning av belastningen på motoraxeln åtföljs av en minskning av cos φ1, vilket förklaras av en ökning av rotorns induktiva motstånd (x2s) på grund av en ökning av slirningen och därför av frekvensen av strömmen i rotorn.

För att förbättra effektfaktorn för induktionsmotorer är det extremt viktigt att motorn alltid går, eller åtminstone en betydande del av tiden, med en belastning nära märklasten. Detta kan endast uppnås med rätt val av motoreffekt. Om motorn går under belastning under en betydande del av tiden, är det lämpligt att minska spänningen U1 som tillförs motorn för att öka cos φ1. Till exempel, i motorer som arbetar när statorlindningen är deltakopplad, kan detta göras genom att återansluta statorlindningarna i stjärna, vilket kommer att få fasspänningen att minska med en faktor. I detta fall minskar statorns magnetiska flöde, och därmed magnetiseringsströmmen, med ungefär en faktor. Dessutom ökar den aktiva komponenten av statorströmmen något. Allt detta bidrar till att öka motorns effektfaktor.

I fig. 3 visar graferna för beroendet av cos φ1, asynkronmotor på lasten, när statorlindningarna är anslutna i stjärna (kurva 1) och delta (kurva 2).

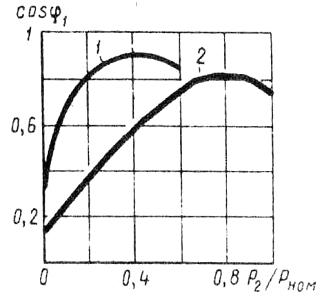
Ris. 3. Beroende av cos φ1 på belastningen vid anslutning av motorns statorlindning med stjärna (1) och delta (2)