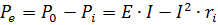Effektbalans i en elektrisk krets
Enligt Joule-Lenz lagen arbete utfört av en likström i ett motstånd,
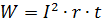
Om en annan omvandlare av elektromagnetisk energi till mekanisk eller kemisk eller annan energiform (elmotor, laddningsbatteri etc.) ingår i den avsedda grenen istället för ett motstånd, kan det arbete som strömmen utför under tiden t beräknas i fallet att om omvandlarens spänning är känd.
I det här fallet tar Joule-Lenz-formeln en annan form:
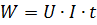
Vid likström ges strömmen som tillförs sektionen av kretsen med resistans r av uttrycket:
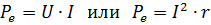
där I, U och r behåller samma betydelse som i Joule-Lenz-formeln.
Strömmen som förbrukas i hela den externa kretsen och strömmen från generatorn är densamma. Effekten som utvecklas av generatorn är alltid större än den som generatorn ger till den externa kretsen, eftersom en del av strömmen går åt för att täcka förluster inuti själva generatorn.
Ett effektbalansuttryck för en enda sluten slinga innehållande en generator med emf E och intern resistans ri och ett motstånd med resistans r kan erhållas från Kirchhoffs ekvation.
För denna krets
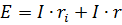
Om båda sidorna av denna ekvation multipliceras med strömmen i kretsen, kommer den resulterande ekvationen att representera effektbalansen i den kretsen
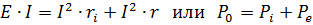
Effekten som utvecklas av generatorn är lika med summan av den effekt som förloras inuti generatorn och ges till den externa kretsen. P0 = EI är den effekt som utvecklas av generatorn, Pe = UI = I2r är den effekt som generatorn ger till den externa kretsen, och Pi — I2ri är den effekt som går förlorad inuti själva generatorn.
När du väljer samma positiva riktningar för strömmen genom den dubbeländade terminalen I och spänningen på den dubbeländade terminalen U, måste den effekt som förbrukas av de två terminalerna, det vill säga produktens användargränssnitt, vara positiv. Om det samtidigt visar sig att användargränssnittet för produkten är negativt, kommer detta att innebära att enheten med två terminaler inte förbrukar elektromagnetisk energi, utan tvärtom är det en generator av elektromagnetisk energi och ger denna energi till elektrisk krets.
Om i en elektrisk krets ett antal enheter med två terminaler avger elektromagnetisk energi till kretsen, absorberar de andra denna energi. I en likströmskrets kan ingen ackumulering av elektromagnetisk energi ske. Därför måste summan av den effekt som förbrukas i passiva tvåterminalsnätverk och den effekt som går förlorad inuti generatorerna vara lika med den algebraiska summan av de effekter som utvecklas av alla generatorer, d.v.s. summan av produkterna EkIk för alla generatorer som arbetar i en krets:
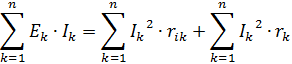
där n — antalet grenar i kedjan.
Balansekvationen som erhålls för en enkel krets som innehåller en generator kan skrivas om genom att uttrycka den effekt som förbrukas i den externa kretsen som den effekt som uttrycks av generatorn och den effekt som går förlorad inuti generatorn: