Impulsström

I olika elektroniska enheter, till exempel i elektronisk utrustning och halvledarutrustning, det vill säga i förstärkare, likriktare, radioapparater, generatorer, tv-apparater, såväl som i kolmikrofoner, telegrafer och många andra enheter, används de ofta krusningsströmmar och spänningar... för att inte upprepa resonemanget två gånger, vi kommer bara att prata om strömmar, men allt som är relaterat till strömmar gäller också för spänningar.

Pulserande strömmar som har en konstant riktning men ändrar sitt värde kan vara olika. Ibland ändras det aktuella värdet från det högsta till det lägsta värdet som inte är noll. I andra fall reduceras strömmen till noll. Om likströmskrets avbryts vid en viss frekvens, så finns det under några tidsintervall ingen ström i kretsen.

I fig. 1 visar grafer över olika vågströmmar. I fig. 1, a, b sker förändringen i strömmarna enl sinusformad kurva, men dessa strömmar bör inte betraktas som sinusformade växelströmmar, eftersom strömmens riktning (tecken) inte ändras. I fig.1 visar c en ström bestående av separata pulser, det vill säga kortlivade "stötar" av ström, separerade från varandra genom pauser av större eller mindre varaktighet, och kallas ofta pulsad ström. Olika pulsade strömmar skiljer sig från varandra i formen och varaktigheten av pulserna, såväl som i upprepningshastigheten.

Det är bekvämt att betrakta en pulserande ström av vilket slag som helst som summan av två strömmar - likström och växelström, kallad term- eller komponentströmmar. Varje pulserande ström har DC- och AC-komponenter. Detta verkar konstigt för många. Faktum är att en pulserande ström är en ström som hela tiden flyter i en riktning och ändrar dess värde.

Hur kan du se att den innehåller växelström som ändrar riktning? Men om två strömmar - direkt och växelström - passerar samtidigt genom samma tråd, visar det sig att en pulserande ström kommer att flyta i den tråden (fig. 2). I detta fall bör växelströmmens amplitud inte överstiga likströmsvärdet. Likström och växelström kan inte flyta separat genom ledningen. De lägger till ett allmänt flöde av elektroner som har alla egenskaper hos en pulserande ström.

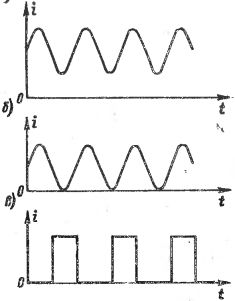
Ris. 1. Grafer över olika vågströmmar

Tillägget av AC- och DC-strömmar kan visas grafiskt. I fig. 2 visar graferna för en likström lika med 15 mA och en växelström med en amplitud på 10 mA. Om vi ​​summerar värdena för dessa strömmar för enskilda tidpunkter, med hänsyn till strömmarnas riktningar (tecken), får vi vågströmsgrafen som visas i fig. 2 med en fet linje. Denna ström varierar från ett lågt värde på 5 mA till ett högt värde på 25 mA.

Den övervägda additionen av strömmar bekräftar giltigheten av representationen av den pulserande strömmen som summan av lik- och växelströmmar. Riktigheten av denna representation bekräftas också av det faktum att med hjälp av vissa enheter är det möjligt att separera komponenterna i denna ström från varandra.

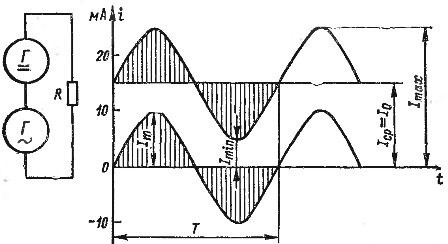
Ris. 2. Erhålla en pulserande ström genom att lägga till lik- och växelström.

Det bör betonas att vilken ström som helst alltid kan representeras som summan av flera strömmar. Till exempel kan en ström på 5 A betraktas som summan av strömmar 2 och 3 A som flyter i en riktning, eller summan av strömmar 8 och 3 A som flyter i olika riktningar, det vill säga skillnaden mellan strömmar 8 och 3 A. Det är inte svårt att hitta andra kombinationer av två eller flera strömmar som ger totalt 5 A.

Här finns en fullständig likhet med principen om addition och nedbrytning av krafter. Om två lika riktade krafter verkar på något föremål kan de ersättas med en gemensam kraft. Krafter som verkar i motsatta riktningar kan ersättas med en enhetsskillnad. Omvänt kan en given kraft alltid betraktas som summan av motsvarande lika riktade krafter eller skillnaden mellan motsatt riktade krafter.

Det är inte nödvändigt att dekomponera lik- eller sinusformade växelströmmar till komponentströmmar. Om vi ​​ersätter den pulserande strömmen med summan av lik- och växelström, då genom att tillämpa de kända lagarna för lik- och växelström på dessa komponentströmmar, är det möjligt att lösa många problem och göra de nödvändiga beräkningarna relaterade till pulserande ström.

Konceptet med pulserande ström som summan av lik- och växelström är konventionellt.Det kan naturligtvis inte antas att lik- och växelströmmarna vid vissa tidsintervall verkligen flyter mot varandra längs tråden. Faktum är att det inte finns två motsatta flöden av elektroner.

I verkligheten är en pulserande ström en enda ström som ändrar sitt värde över tiden. Det är mer korrekt att säga att den pulserande spänningen eller pulserande EMF kan representeras som summan av de konstanta och variabla komponenterna.

Till exempel, i FIG. 2 visar hur algebraiskt den konstanta emk för en generator adderas till den variabla emk för en annan generator. Som ett resultat har vi en pulserande EMF som orsakar motsvarande pulserande ström. Villkorligt kan det dock anses att en konstant EMF skapar en likström i kretsen, och en växel EMF - en växelström, som, när den summeras, bildar en pulserande ström.

Varje pulserande ström kan karakteriseras av de maximala och lägsta värdena för Itax och Itin, såväl som dess konstanta och variabla komponenter. Den konstanta komponenten betecknas med I0. Om växelkomponenten är en sinusformad ström, betecknas dess amplitud med It (alla dessa kvantiteter visas i fig. 2).

Det ska inte förväxlas med It och Itax. Det maximala värdet för strömvågen Imax bör inte heller kallas amplituden. Termen amplitud avser vanligtvis endast växelströmmar. När det gäller den pulserande strömmen kan vi bara prata om amplituden för dess variabla komponent.

Den konstanta komponenten av den pulserande strömmen kan kallas dess medelvärde Iav, det vill säga det aritmetiska medelvärdet. Faktum är att om vi betraktar förändringarna under en period av den pulserande strömmen som visas i fig.2 syns tydligt följande: i den första halvcykeln läggs ett antal värden till 15 mA-strömmen genom att variera strömkomponenten, varierande från 0 till 10 mA och tillbaka till 0, och i den andra halvan -cykel, exakt samma strömvärden subtraheras från strömmen 15 mA.

Därför är strömmen på 15 mA verkligen medelvärdet. Eftersom ström är överföringen av elektriska laddningar genom trådens tvärsnitt, så är Iav värdet på en sådan likström som under en period (eller under ett helt antal perioder) bär samma mängd elektricitet som denna pulserande ström .

För sinusformad växelström är värdet på Iav per period noll eftersom mängden elektricitet som passerar genom ledarens tvärsnitt under en halvperiod är lika med mängden elektricitet som passerar i motsatt riktning under en annan halvperiod. På graferna över strömmar som visar strömmens i beroende av tiden t, uttrycks mängden elektricitet som strömmen bär med arean av figuren som begränsas av strömkurvan, eftersom mängden elektricitet bestäms av produkt som det.

För en sinusformad ström är ytorna för de positiva och negativa halvvågorna lika.I den pulserande strömmen som visas i fig. 2, under den första halvperioden läggs mängden elektricitet som transporteras av AC-komponenten till mängden elektricitet som bärs av nuvarande Iav (skuggat område i figuren). Och under den andra halvcykeln dras exakt samma mängd el ut. Som ett resultat överförs samma mängd elektricitet under hela perioden som med en enda likström Iav, det vill säga arean av rektangeln Iav T är lika med området som begränsas av vågströmskurvan.

Således bestäms den konstanta komponenten eller medelvärdet av strömmen av överföringen av elektriska laddningar genom trådens tvärsnitt.

Den aktuella ekvationen som visas i fig. 2 ska självklart skrivas i följande form:

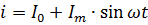
Effekten av den pulserande strömmen måste beräknas som summan av effekterna av dess komponentströmmar. Till exempel, om strömmen som visas i fig. 2, passerar genom ett motstånd med motstånd R, då är dess effekt

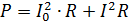
där I = 0,7Im är rms-värdet för den variabla komponenten.

Du kan introducera konceptet med rms-värdet för vågströmmen Id. Effekten beräknas på vanligt sätt:

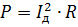
Genom att likställa detta uttryck med det föregående och reducera det med R får vi:

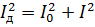
Samma samband kan erhållas för påfrestningar.