Elektriska filter — definition, klassificering, egenskaper, huvudtyper

Industriella energikällor ger praktiska sinusformade spänningskurvor… Samtidigt skiljer sig i ett antal fall växelströmmar och spänningar, som är periodiska, kraftigt från harmoniska.

Elektriska filter kan användas för att jämna ut spänningsvågor i likriktare, demodulatorer som omvandlar amplitudmodulerade högfrekventa oscillationer till relativt långsamma förändringar i signalspänning och andra liknande enheter.

I det enklaste fallet kan du begränsa dig till seriell anslutning med lasten induktorer, vars resistans ökar med ökande harmonisk ordning och är relativt liten för lågfrekventa svängningar och ännu mer för den konstanta komponenten. Det är mer effektivt att använda U-formade, T-formade och L-formade filter.

Grundläggande definitioner och klassificering av elfilter

Filtrets selektivitet är dess förmåga att välja ett visst intervall av frekvenser som är inneboende i den användbara signalen från hela frekvensspektrumet av strömmar som kommer in i dess ingång.

För att erhålla god selektivitet måste filtret passera strömmar vid frekvenser som är inbyggda i den önskade signalen med minimal dämpning och ha maximal dämpning för strömmar vid alla andra frekvenser. I enlighet med detta filter kan följande definition ges.

Ett elektriskt filter kallas en fyrpolig enhet som överför strömmar i ett visst frekvensband med liten dämpning (bandbredd), och strömmar med frekvenser utanför detta band — med hög dämpning eller, som det brukar sägas, inte passerar (icke- överföringsband).

Enligt strukturen av kretsarna är filter uppdelade i kedje- (kolumn) och bryggfilter. Kedjefilter är filter tillverkade enligt T-, P- och L-formade bryggkretsar. Bryggfilter är filter tillverkade på en bryggkrets.

Beroende på elementens karaktär är filtren indelade i:

• LC — element som är induktans och kapacitans;

• RC — element som är aktiva motstånd och kapaciteter;

• resonator — vars element är resonatorer.

Beroende på närvaron av energikällor i filterkretsen är de indelade i:

• passiv — innehåller inte energikällor i kretsen;

• aktiv — innehåller energikällor i kretsen i form av en lampa eller kristallförstärkare; kallas ibland filter för aktiva element.

För en fullständig karakterisering av filterprestanda är det nödvändigt att känna till dess elektriska egenskaper, som inkluderar frekvensberoende för dämpning, fasförskjutning och karakteristisk impedans.

Det bästa är ett filter som, med ett minimum antal element, har:

• den maximala brantheten hos dämpningskarakteristiken;

• hög dämpning i icke-sändningsbandet;

• minimal och konstant dämpning i passbandet;

• maximal konstans för den karakteristiska impedansen i passbandet;

• linjär fasrespons;

• möjligheten till enkel och smidig justering av frekvensbandet och dess bredd;

• konstans av egenskaper som inte beror på: spänningar (strömmar) som verkar vid filteringången, temperatur och luftfuktighet i omgivningen, såväl som påverkan av externa elektriska och magnetiska störningar;

• förmåga att arbeta i olika frekvensområden;

• storlek, vikt och kostnad för filtret måste hållas till ett minimum.

Tyvärr finns det ingen enda elementär typ av filter vars egenskaper uppfyller alla dessa krav. Därför, beroende på de specifika förhållandena, används sådana typer av filter, vars egenskaper bäst uppfyller de tekniska kraven. Mycket ofta är det nödvändigt att applicera filter på komplexa kretsar som består av elementära anslutningar av olika typer.

De vanligaste typerna av filter

I fig. 1 visar diagrammet över ett enkelt L-format filter med induktor L och kondensator C kopplade mellan mottagaren rpr och likriktaren V.

Växelströmmarna vid alla frekvenser möter en betydande induktorresistans, och en parallellkopplad kondensator passerar de kvarvarande högfrekventa strömmarna längs den parallella grenen. Detta minskar avsevärt spänningsrippel i lasten. rNS.

Filter som består av två eller flera liknande länkar kan också användas. Ibland används enkla filter med resistorer istället för induktorer.

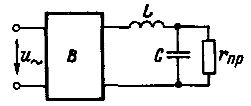
Ris. 1.Det enklaste utjämnande L-formade elfiltret

Mer avancerade är resonansfiltren de använder resonansfenomen.

När induktorn och kondensatorn är seriekopplade, när fwL = 1 / (kwV), kommer kretsen att ha den högsta konduktiviteten (aktiv) vid frekvensen fw och ganska höga konduktiviteter i frekvensbandet nära resonansen. Denna krets är ett enkelt bandpassfilter.

När induktorn och kondensatorn är parallellkopplade kommer en sådan krets att ha den lägsta konduktiviteten vid resonansfrekvensen och relativt låg konduktivitet i frekvensbandet nära resonansfrekvensen. Ett sådant filter är ett blockeringsfilter för ett visst frekvensband.

För att förbättra prestandan hos ett enkelt bandpassfilter är det möjligt att använda ett schema (fig. 2) där en induktor och en kondensator är anslutna parallellt med varandra parallellt med mottagaren. En sådan krets är också avstämd i resonans med getternas frekvens och uppvisar ett mycket högt motstånd för strömmar i det valda frekvensbandet och mycket mindre motstånd för strömmar med andra frekvenser.

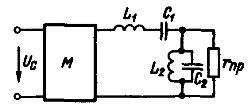
Ris. 2. Schematisk bild av ett enkelt bandpassfilter

Ett liknande filter kan användas i modulatorer som producerar modulerade oscillationer vid en specifik frekvens. En lågfrekvent signalspänning Uc tillförs modulatorn M, som omvandlas till modulerade högfrekventa svängningar, och filtret separerar spänningen från den erforderliga frekvensen, som matas till lasten rNS.

Antag till exempel att en icke-sinusformad växelström flyter genom kretsen och att mycket stora tredje och femte övertonsströmmar ska elimineras från mottagarströmkurvan.Därefter kommer vi växelvis att inkludera två kretsar som är avstämda till resonans för den tredje och femte övertonen i kretsen (fig. 3, a).

En vänsterlinjeimpedans avstämd till resonans för en frekvens på 3w kommer att vara mycket stor för den frekvensen och liten för alla andra övertoner; en liknande roll spelas av den högra kretsen som är avstämd till resonans för frekvens 5w... Därför kommer strömkurvan för ingångsmottagaren nästan inte att innehålla den tredje och femte övertonen (fig. 3, b), som kommer att undertryckas av filtrera.

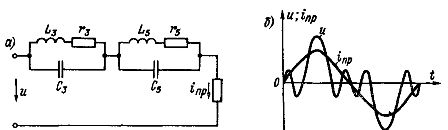
Ris. 3. Schema med seriekopplade resonanskretsar avstämda till resonans för tredje och femte övertonen: a — kretsschema; b — Kurvor för spänning och krets och ström inp för mottagaren

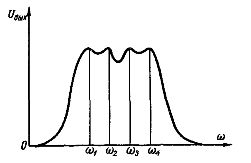
Ris. 4. Bandpassfiltrets utspänningskurva

I vissa fall utförs mer sofistikerade bandpassfilter, liksom cut-off filter som passerar eller inte passerar svängningar som börjar vid en viss frekvens. Sådana filter består av T-formade eller U-formade anslutningar.

Funktionsprincipen för filter är att i frekvensbandet av frekvenser, till exempel ett bandpassfilter, uppstår resonans vid n + 1 frekvenser, där n är antalet anslutningar. En kurva Uout = f (w) för ett sådant filter som består av tre anslutningar visas i fig. 4. Resonans uppstår vid frekvenserna w1,w2, w3 och w4.

Se även om detta ämne: Strömfilter ochIn- och utgångsfilter för frekvensomformare