Yteffekt och närhetseffekt

Ledarens resistans mot likström bestäms av den välkända formeln ro =ρl / S.

Detta motstånd kan också bestämmas genom att känna till storleken på den konstanta strömmen IО och effekten PO:

ro = PO / AzO2

Det visar sig att i en växelströmskrets är motståndet r för samma ledare större än motståndets konstantström: r> rО

Detta motstånd r i motsats till likströmsmotståndet rO och kallas aktivt motstånd. Ökningen av trådresistans förklaras av det faktum att med växelström är strömtätheten inte densamma på olika punkter i trådens tvärsnitt. Jag har ledarytor, strömtätheten är högre än med likström, och mitten är mindre.

Vid hög frekvens uppträder oregelbundenheterna så skarpt att strömtätheten i en betydande central renhet av ledarens tvärsnitt är praktiskt taget noll. Strömmen passerar endast i ytskiktet, varför detta fenomen kallas yteffekten.

Således leder yteffekten till en minskning av ledarens tvärsnitt genom vilken strömmen flyter (aktivt tvärsnitt), och därför till en ökning av dess motstånd jämfört med likströmsresistansen.

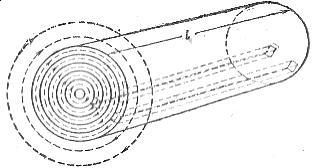
För att förklara orsaken till yteffekten, föreställ dig en cylindrisk ledare (fig. 1), bestående av ett stort antal elementära ledare med samma tvärsnitt, i omedelbar närhet av varandra och arrangerade i koncentriska lager.

Motstånden för dessa ledningar mot likström, som hittas av formeln ρl / S kommer att vara desamma.

Ris. 1. Magnetfältet hos en cylindrisk ledare.

En elektrisk växelström skapar ett växelmagnetiskt fält runt varje tråd (Fig. 1). Uppenbarligen är den elementära ledaren som är belägen närmare axeln omgiven av en stor magnetisk flödesytledare, därför har den förra en högre induktans och induktiv reaktans än den senare.

Vid samma spänning i ändarna av elementära ledningar med längd l som ligger längs axeln och på ytan, är strömtätheten i den första mindre än i den andra.

Skillnaden v strömtätheten längs axeln och längs ledarens periferi ökar med en ökning av diametern på ledaren d, ledningsförmågan hos materialet γ, materialets magnetiska permeabilitet μ och AC-frekvens.

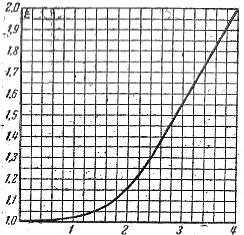
Förhållandet mellan det aktiva motståndet för en ledare r och dess motstånd vid. likström rО kallas hudeffektskoefficienten och betecknas med bokstaven ξ (xi), därför kan koefficienten ξ bestämmas från grafen i fig. 2, som visar beroendet av ξ på produkten d och √γμμое.

Ris. 2. Diagram för bestämning av hudeffektkoefficienten.

Vid beräkning av denna produkt ska d uttryckas i cm, γ — i 1 / ohm-cm, μo — v gn/ cm och f = i Hz.

Ett exempel. Det är nödvändigt att bestämma koefficienten för hudeffekten för Jag är en kopparledare med en diameter på d= 11,3 mm (S = 100 mm2) vid en frekvens på f = 150 Hz.

Bra jobbat.

Enligt grafen i fig. 2 finner vi ξ = 1,03

Ojämn strömtäthet i en ledare uppstår också på grund av påverkan av strömmar i angränsande ledare. Detta fenomen kallas för närhetseffekten.

Med tanke på magnetfältet för strömmar i samma riktning i två parallella ledare, är det lätt att visa att de elementära ledare som tillhör olika ledare, som är längst från varandra, är förbundna med det minsta magnetiska flödet, därför strömtätheten i dem är den högsta. Om strömmarna i parallella ledningar har olika riktning, kan det visas att en hög strömtäthet observeras i de elementära ledningar som tillhör olika ledningar som ligger närmast varandra.