RMS-värden för ström och spänning
Den sinusformade växelströmmen har olika momentana värden under perioden. Det är naturligt att ställa frågan, vilket värde av ström kommer att mätas med amperemetern som ingår i kretsen?
Vid beräkning av växelströmskretsar, såväl som elektriska mätningar, är det obekvämt att använda momentana eller amplitudvärden för strömmar och spänningar, och deras medelvärden under en period är noll. Dessutom kan den elektriska effekten av en periodiskt föränderlig ström (mängden värme som frigörs, den perfekta driften etc.) inte uppskattas av amplituden av denna ström.
Det mest bekväma var introduktionen av begreppen för de så kallade effektiva värdena för ström och spänning... Dessa koncept är baserade på strömmens termiska (eller mekaniska) verkan, som inte beror på dess riktning.
Rotmedelkvadratvärde för växelström - detta är värdet på likström vid vilken under växelströmsperioden samma mängd värme frigörs i ledaren som under växelström.
För att utvärdera vidtagna åtgärder växelström, kommer vi att jämföra dess handlingar med den termiska effekten av likström.
Likström P A som passerar genom motstånd r blir P = P2r.
Växelström uttrycks som den genomsnittliga effekten av den momentana effekten Az2r över hela perioden eller medelvärdet av (I am x sinωT)2 NS r för samma tid.
Låt medelvärdet av t2 för perioden vara M. Jämför effekten av likström och effekt av växelström, vi har: Az2r = Mr -n, varav Az = √M,
Storheten I kallas växelströmmens effektiva värde.
Medelvärdet för i2 vid växelström bestäms enligt följande.
Låt oss konstruera en sinusformad strömkurva. Genom att kvadrera varje momentant strömvärde får vi en P mot tiden kurva.
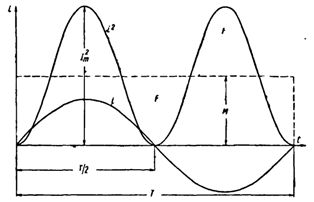AC rms värde
Båda halvorna av denna kurva ligger ovanför den horisontella axeln, eftersom de negativa strömmarna (-i) under andra halvan av perioden, i kvadrat, ger positiva värden.
Konstruera en rektangel med basen T och arean lika med arean som begränsas av kurvan i2 och horisontell axel. Höjden på rektangeln M kommer att motsvara medelvärdet av P för perioden. Detta periodvärde, beräknat med högre matematik, kommer att vara lika med 1/2 I2m... Därför är M. = 1/2 I2m
Eftersom rms-värdet Im växelström är Im = √M, så slutligen I = Im / √2
På liknande sätt har förhållandet mellan rms och amplitudvärdena för spänningen U och E formen:
U = Um / √2E = Em / √2
Variablernas effektiva värden indikeras med versaler utan teckningar (I, U, E).
Baserat på ovanstående kan vi säga att det effektiva värdet av en växelström är lika med en sådan likström, som, som passerar genom samma motstånd som växelströmmen, avger samma mängd energi samtidigt.
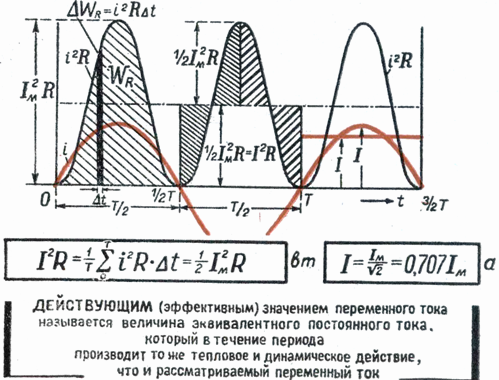
Elektriska mätinstrument (amperemeter, voltmetrar) som ingår i en växelströmkrets indikerar de effektiva värdena för ström eller spänning.
När du konstruerar vektordiagram är det bekvämare att skjuta upp inte amplituden, utan de effektiva värdena för vektorerna. För detta reduceras vektorernas längder med √2 en gång. Detta ändrar inte placeringen av vektorerna på diagrammet.