Teori om automater, ändliga automater
Strukturen, designen, funktionsprincipen för olika maskiner bestäms till stor del av dess funktionella syfte. Skilj mellan tekniska, transport-, dator-, militära och andra maskiner. Hela automatiska komplex som är utformade för att utföra komplexa tekniska processer är allmänt introducerade i olika branscher. Automater är designade och byggda som utför olika logiska funktioner (logiska maskiner).
Teori om automater — sektionen för cybernetik, som uppstod under påverkan av kraven på tekniken för digitala datorer och styrmaskiner. Diskreta automater som studeras i automatteorin är abstrakta modeller av verkliga system (både tekniska och biologiska) som behandlar diskret (digital) information i diskreta tidssteg.
Automatteorin bygger på exakta matematiska begrepp som formaliserar intuitiva idéer om automatens funktion (beteende) och om dess struktur (inre struktur).
I detta fall förstås informationsomvandling alltid som en operation som omvandlar inmatningssekvenser sammansatta av bokstäver från inmatningsalfabetet till utdatasekvenser sammansatta av bokstäver från utgående alfabet.
Apparaterna för matematisk logik, algebra, sannolikhetsteori, kombinatorik och grafteori används i stor utsträckning.
Problemet med teorin om automater i några av dess delar (strukturteorin om automater) växte från teorin om relä-kontaktkretsar, som började ta form i slutet av 1930-talet. inkluderande metoder för logisk algebra.

I den strukturella teorin om automater studeras olika typer av scheman, utformade för att beskriva hur en komplex automat skapas av enklare komponenter (element) korrekt kopplade i ett system.
En annan riktning, som kallas den abstrakta teorin om automater, studerar beteendet hos automater (det vill säga arten av omvandlingen av information som utförs av dem), samtidigt som den abstraherar från detaljerna i deras interna struktur, och uppstod på 1950-talet.
Inom ramen för den abstrakta teorin om automater är innehållet i begreppen "automat" och "maskin" i huvudsak uttömt av standardbeskrivningen av omvandlingen av information som utförs av en automat. En sådan transformation kan vara deterministisk, men den kan också vara sannolik.
De mest studerade är deterministiska maskiner (automater), som inkluderar finita automater - huvudobjektet för studien i automatteorin.
En finita tillståndsmaskin kännetecknas av en begränsad mängd minne (antalet interna tillstånd) och definieras med hjälp av en övergångsfunktion.Med viss rimlig idealisering kan alla moderna matematiska maskiner och till och med hjärnan, ur deras funktionssynpunkt, betraktas som ändliga automater.
Termerna "sekventiell maskin", "Milly-automat", "Moore-automat" används i litteraturen (och inte enhetligt av alla författare) som synonymer till termen "ändlig automat" eller för att betona vissa egenskaper i en ändlig övergångsfunktion. automat.
Automata med obegränsat minne är en Turing-maskin som kan utföra (potentiellt) vilken effektiv informationstransformation som helst. Begreppet "Turing-maskin" uppstod tidigare än begreppet "finite state machine" och studeras huvudsakligen inom teorin om algoritmer.
Abstrakt automatteori är nära besläktad med välkända algebraiska teorier, till exempel semigruppteori. Ur en tillämpad synvinkel är resultaten som karaktäriserar omvandlingen av information i en automat i termer av minnesstorlek av intresse.
Detta är till exempel fallet i problem med experiment på automater (verk av E.F. Moore, etc.), där en eller annan information om automatens övergångsfunktioner eller om kapaciteten hos dess minne erhålls från resultaten av experiment.
En annan uppgift är att beräkna perioderna för utmatningssekvenserna, baserat på tillgänglig information om automatens minnesstorlek och ingångssekvensernas perioder.
Av stor betydelse är utvecklingen av metoder för att minimera minnet av finita tillståndsmaskiner och studera deras beteende i slumpmässiga miljöer.
I abstrakt automatteori är syntesproblemet följande.När det gäller något tydligt formaliserat språk är villkoren skrivna för beteendet hos den designade automaten (för händelsen representerad i automaten). I det här fallet är det nödvändigt att utveckla metoder som enligt varje skriftligt tillstånd:
1) ta reda på om det finns en sådan tillståndsmaskin att informationen som omvandlas av den uppfyller detta villkor;
2) om ja, då konstrueras övergångsfunktionerna för en sådan finita tillståndsmaskin eller dess minnesstorlek uppskattas.
Lösningen av syntesuppgiften i en sådan formulering förutsätter det preliminära skapandet av ett bekvämt språk för att registrera driftsförhållandena för en automat med bekväma algoritmer för övergången från inspelning till transitiva funktioner.
I den strukturella teorin om automater består syntesproblemet i att konstruera en kedja av element av en given typ som realiserar en finit automat given av dess övergångsfunktioner. I det här fallet anger de vanligtvis ett optimalitetskriterium (till exempel det minsta antalet element) och försöker få ett optimalt schema.
Som det visade sig senare innebär detta att några av de metoder och koncept som utvecklats tidigare i relation till reläkontaktkretsar är tillämpliga på kretsar av annan typ.
I samband med utvecklingen av elektronisk teknik är systemen mest utbredda av funktionella element (logiska nätverk). Ett specialfall av logiska nätverk är abstrakta neurala nätverk, vars element kallas neuroner.
Många syntesmetoder har utvecklats, beroende på typen av kretsar och omvandlingen av information som de är avsedda för (Syntes av reläanordningar).
Se -Minimering av kombinationskretsar, Carnot-kartor, kretssyntes
Finite state-maskin — En matematisk modell av ett styrsystem med en fast (som inte kan öka under drift) minnesstorlek.
Konceptet med en finita tillståndsmaskin är en matematisk abstraktion som kännetecknar de allmänna egenskaperna hos en uppsättning styrsystem (till exempel en multi-loop reläanordning). Alla sådana system har gemensamma egenskaper som är naturliga att acceptera som definitionen av en finit automat.
Varje färdig automat har en ingång utsatt för yttre påverkan och inre element. För både input och interna element finns det ett fast antal diskreta tillstånd som de kan ta.
Förändringen i tillstånden för de ingående och interna elementen sker vid diskreta ögonblick i tiden, intervallen mellan vilka kallas tick. Det interna tillståndet (tillståndet för interna) i slutet av bandet bestäms helt av det interna tillståndet och tillståndet för ingången i början av bandet.
Alla andra definitioner av en finit automat kan reduceras till denna egenskap, i synnerhet definitioner som antar att en finit automat har en utgång som beror på automatens interna tillstånd vid en given tidpunkt.
När det gäller en sådan egenskap är arten av dess ingångar och interna tillstånd irrelevant för beskrivningen av en komplett automat. Istället för ingångar och tillstånd kan du bara titta på deras nummer i en slumpmässig numrering.
Tillståndsmaskinen kommer att ställas in om beroendet av dess interna tillståndsnummer på det tidigare interna tillståndsnumret och det tidigare inmatade tillståndsnumret specificeras. En sådan uppgift kan vara i form av ett finalbord.
Ett annat vanligt sätt att definiera en komplett automat är konstruktionen av den sk övergångsdiagram. Ingångstillstånd kallas ofta för enkla ingångar, och interna tillstånd är helt enkelt tillstånd.
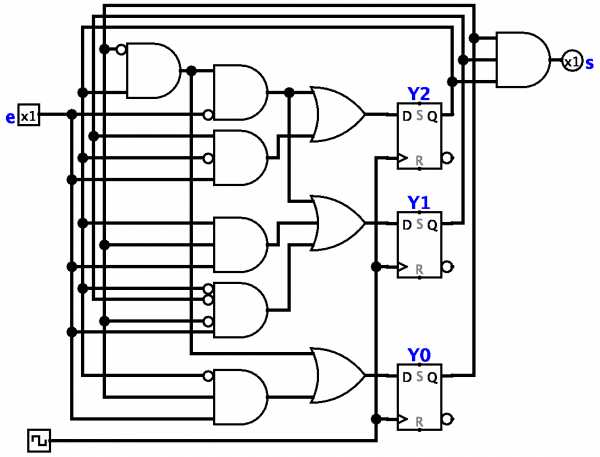
En finita tillståndsmaskin kan vara en modell av både tekniska anordningar och vissa biologiska system. Automater av den första typen är till exempel reläapparater och olika elektroniska datorer, inkl. programmerbara logiska styrenheter.
I fallet med en reläanordning spelas rollen av ingångstillstånd av kombinationer av tillstånd för de känsliga elementen i reläanordningen (varje kombination av sådana tillstånd är ett "komplext tillstånd", kännetecknat av en indikation av alla känsliga element i reläanordningen dessa diskreta tillstånd som de har i ett givet ögonblick). På liknande sätt fungerar kombinationer av tillstånd av mellanliggande element i en reläanordning som interna tillstånd.
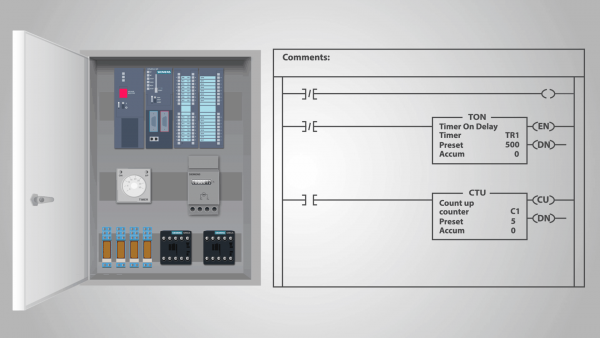
En programmerbar logisk styrenhet (PLC) är ett exempel på en reläfunktionsenhet som kan kallas en fristående tillståndsmaskin.
Faktum är att när programmet väl har matats in i PLC:n och regulatorn har börjat beräkna, utsätts det inte för yttre påverkan och varje efterföljande tillstånd bestäms helt av dess tidigare tillstånd. Vi kan anta att ingången har samma tillstånd i varje klockcykel.
Omvänt kallas varje finita tillståndsmaskin som har det enda möjliga ingångstillståndet naturligt autonom, eftersom den yttre miljön i detta fall inte bär någon information som styr dess beteende.
Se även:
Användningen av mikroprocessorsystem inom elektroteknik på exemplet med användningen av PLC