Tidskonstanten för en elektrisk krets - vad det är och var det används

Periodiska processer är inneboende i naturen: dag följs av natt, den varma årstiden ersätts av kyla, etc. Perioden för dessa händelser är nästan konstant och kan därför strikt bestämmas. Dessutom har vi rätt att hävda att de periodiska naturliga processer som nämns som exempel inte försämras, åtminstone vad gäller en persons livslängd.

Men inom teknik, inom elektroteknik och elektronik, speciellt, är inte alla processer periodiska och kontinuerliga. Vanligtvis ökar vissa elektromagnetiska processer först och minskar sedan. Ofta är materia bara begränsad till fasen av början av svängningen, som inte hinner ta fart på riktigt.

Ganska ofta inom elektroteknik kan man hitta så kallade exponentiella transienter, vars essens är att systemet helt enkelt strävar efter att nå något jämviktstillstånd, som så småningom ser ut som ett vilotillstånd. En sådan övergång kan vara antingen ökande eller minskande.

Den yttre kraften bringar först det dynamiska systemet ur jämvikt och förhindrar sedan inte det naturliga återgången av detta system till sitt ursprungliga tillstånd. Denna sista fas är den så kallade övergångsprocessen, som kännetecknas av en viss varaktighet. Dessutom är processen att obalansera systemet också en övergående process med en karakteristisk varaktighet.

På ett eller annat sätt, tidskonstanten för den transienta processen, kallar vi dess tidskaraktäristik, som bestämmer tiden efter vilken en viss parameter i denna process kommer att ändra tiderna «e», det vill säga den kommer att öka eller minska med cirka 2,718 gånger jämfört med utgångsläget.

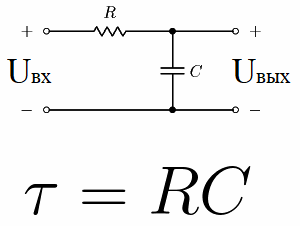
Betrakta till exempel en elektrisk krets som består av en likspänningskälla, en kondensator och ett motstånd. Denna typ av krets där ett motstånd är seriekopplat med en kondensator kallas en RC-integreringskrets.

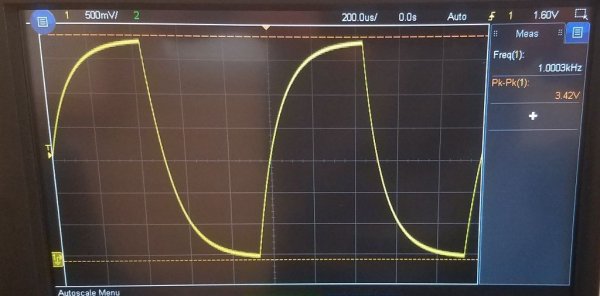
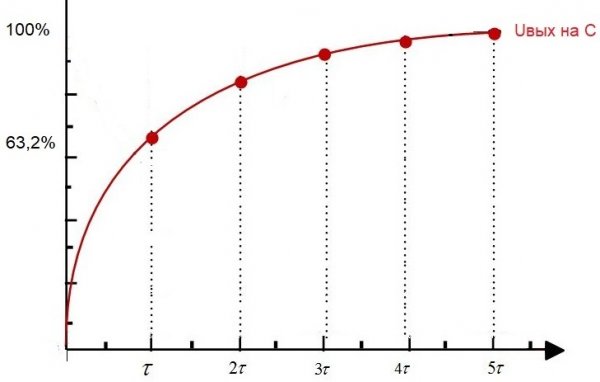
Om i det första ögonblicket för att leverera ström till en sådan krets, det vill säga att ställa in en konstant spänning Uin vid ingången, så kommer Uout - spänningen i kondensatorn att börja växa exponentiellt.

Efter tid t1 kommer kondensatorspänningen att nå 63,2 % av ingångsspänningen. Så, tidsintervallet från det initiala ögonblicket till t1 är tidskonstanten för denna RC-krets.

Denna kedjekonstant kallas «tau», mätt i sekunder och indikerad med dess motsvarande grekiska bokstav. Numeriskt, för en RC-krets, är det lika med R * C, där R är i ohm och C är i farad.

Integrerande RC-kretsar används inom elektroniken som lågpassfilter när högre frekvenser måste stängas av (undertryckas) och lägre frekvenser måste passeras igenom.

I praktiken är mekanismen för sådan filtrering baserad på följande princip. För växelström fungerar kondensatorn som ett kapacitivt motstånd, vars värde är omvänt proportionellt mot frekvensen, det vill säga ju högre frekvensen är, desto lägre blir kondensatorns reaktans i ohm.

Därför, om en växelström passerar genom RC-kretsen, kommer, som på spänningsdelarens arm, en viss spänning att falla över kondensatorn, proportionell mot dess kapacitans vid frekvensen av den passerade strömmen.

Om gränsfrekvensen och amplituden för den ingående alternerande signalen är kända, kommer det inte att vara svårt för konstruktören att välja en sådan kondensator och motstånd i RC-kretsen, så att den lägsta (cut-off) spänningen (för cut-off frekvens — den övre gränsen för frekvensen) faller på kondensatorn, eftersom reaktansen går in i delaren tillsammans med ett motstånd.

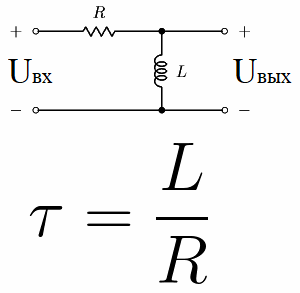
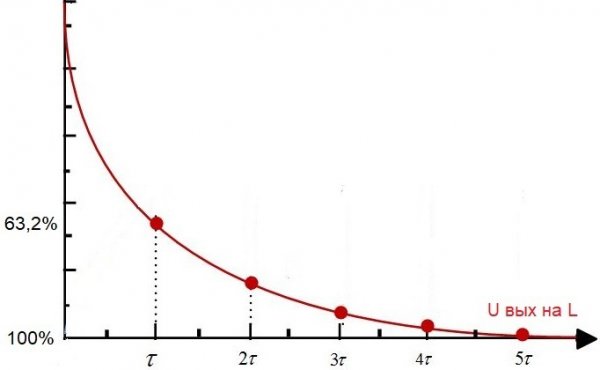
Tänk nu på den så kallade differentieringskretsen. Det är en krets som består av ett motstånd och en induktor kopplade i serie, en RL-krets. Dess tidskonstant är numeriskt lika med L / R, där L är spolens induktans i henries och R är motståndet för motståndet i ohm.

Om en konstant spänning från en källa appliceras på en sådan krets, kommer efter en tid tau spolens spänning att minska jämfört med U in med 63,2 %, det vill säga helt i enlighet med värdet på tidskonstanten för denna elektriska krets .

I AC-kretsar (alternerande signaler) används LR-kretsar som högpassfilter när låga frekvenser måste stängas av (undertryckas) och frekvenser över (över gränsfrekvensen - den nedre frekvensgränsen) - utelämnas.Så ju högre induktans spolen har, desto högre frekvens.

Som i fallet med RC-kretsen som diskuterats ovan används här spänningsdelarprincipen. En högre frekvensström som passerar genom RL-kretsen kommer att resultera i ett större spänningsfall över induktansen L, som med det induktiva motståndet som är en del av spänningsdelaren tillsammans med motståndet. Konstruktörens uppgift är att välja sådana R och L så att spolens minsta (gräns)spänning erhålls exakt vid gränsfrekvensen.