Elektroner beter sig som vågor

Fysiker har länge vetat att ljus är en elektromagnetisk våg. Till denna dag tvivlar ingen på denna position, eftersom ljus tydligt visar alla tecken på vågbeteende: ljusvågor kan överlappa varandra, generera ett interferensmönster, de kan också separera, böja sig runt hinder längs diffraktionstiden.

När vi ser en fågel som går som en anka, simmar som en anka och kvackar som en anka, kallar vi den fågeln för en anka. Så ljuset är elektromagnetisk vågbaserat på objektivt observerade tecken på beteendet hos en sådan våg i ljus.

Men i slutet av 1800- och 1900-talen skulle fysiker börja tala om ljusets "partikelvågsdualism". Det visar sig att kunskapen om att ljus är en elektromagnetisk våg inte är allt som vetenskapen vet om ljus. Forskare har upptäckt en mycket intressant egenskap i ljus.

Det visar sig att ljus på något sätt manifesterar sig SOM beteendet hos en ström av partiklar på något sätt.Det visade sig att energin som bärs av ljuset, efter att ha räknats under en viss tidsperiod av en speciell detektor, visar sig vara sammansatt av enskilda (hela) bitar.

Därför blev det sant att ljusets energi är diskret, eftersom den så att säga är sammansatt av individuella partiklar - "kvanta", det vill säga av de minsta hela delar av energi. En sådan ljuspartikel, som bär en enhet (eller kvantum) energi, kom att kallas en foton.

Energin för en foton hittas med följande formel:

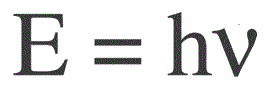
E — fotonenergi, h — Plancks konstant, v — frekvens.

Den tyske fysikern Max Planck etablerade först experimentellt faktumet om ljusvågens diskrethet och beräknade värdet på konstanten h, som visas i formeln för att hitta energin hos enskilda fotoner. Detta värde visade sig vara: 6,626 * 10-34 J * s. Planck publicerade resultaten av sitt arbete i slutet av 1900-talet.

Tänk till exempel en lila stråle. Frekvensen för sådant ljus (f eller v) är 7,5 * 1014 Hz Plancks konstant (h) är 6,626 * 10-34 J * s. Det betyder att energin hos fotonen, (E), som är karakteristisk för färgen violett, är 5 * 10-19 J. Detta är en så liten del av energin att den är mycket svår att fånga.

Föreställ dig en bergsbäck — den flyter som en enhet, och det är omöjligt att se med blotta ögat att bäcken faktiskt består av enskilda vattenmolekyler. Idag vet vi dock att det makroskopiska objektet – flödet – faktiskt är diskret, det vill säga består av individuella molekyler.

Det betyder att om vi kan placera en molekylräknare bredvid strömmen för att räkna vattenmolekylerna som passerar när strömmen strömmar, kommer detektorn alltid bara att räkna hela antal vattenmolekyler, inte partiella sådana.

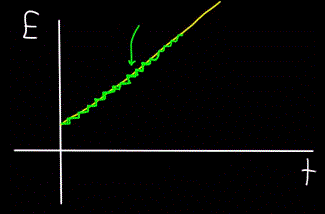
På liknande sätt kommer grafen för fotonen Es totala energi, beräknad vid tidpunkten t — alltid att visa sig inte vara linjär (gul figur), utan stegvis (grön figur):

Så, fotoner rör sig, de bär energi, därför har de fart. Men en foton har ingen massa. Hur kan du då hitta fart?

Faktum är att för objekt som rör sig med hastigheter nära ljusets hastighet, är den klassiska formeln p = mv helt enkelt otillämplig. För att förstå hur man hittar fart i detta ovanliga fall, låt oss vända oss till speciell relativitet:

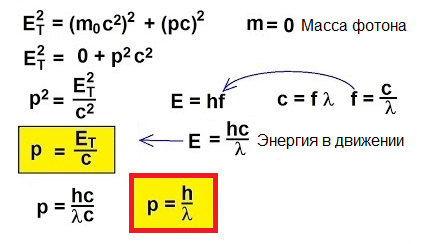
1905 förklarade Albert Einstein från denna synvinkel fotoelektrisk effekt… Vi vet att metallplattan har elektroner inom sig, som inuti den attraheras av atomernas positivt laddade kärnor och därför hålls kvar i metallen. Men om du lyser en sådan platta med ljus av en viss frekvens, då kan du slå ut elektroner ur plattan.

Det är som om ljus beter sig som en ström av partiklar med rörelsemängd. Och även om en foton inte har någon massa, interagerar den på något sätt med en elektron i en metall, och under vissa förhållanden kan en foton slå ut en elektron.

Så om en foton som faller in på plattan har tillräckligt med energi, kommer elektronen att slås ut ur metallen och röra sig ut ur plattan med hastighet v. En sådan utslagen elektron kallas en fotoelektron.

Eftersom den utslagna elektronen har en känd massa m kommer den att ha en viss kinetisk energi mv.

Fotonens energi omvandlas, när den verkade på metallen, till energin för elektronens utträde från metallen (arbetsfunktion) och till elektronens kinetiska energi, som den utslagna elektronen börjar röra sig på. ur metallen och lämnar den.

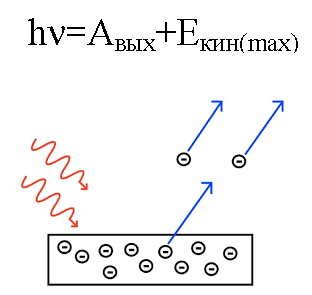
Antag att en foton med känd våglängd träffar ytan på en metall för vilken arbetsfunktionen (för en elektron från metallen) är känd. I detta fall kan den kinetiska energin för en elektron som emitteras från en given metall lätt hittas, liksom dess hastighet.

Om fotonens energi inte är tillräcklig för att elektronen ska utföra arbetsfunktionen, kan elektronen helt enkelt inte lämna ytan på den givna metallen och fotoelektronen bildas inte.

1924, en fransk fysiker Louis de Broglie lägga fram en banbrytande idé enligt vilken inte bara fotoner av ljus utan elektroner själva kan bete sig som vågor. Forskaren härledde till och med en formel för elektronens hypotetiska våglängd. Dessa vågor kallades senare "de Broglie-vågor".

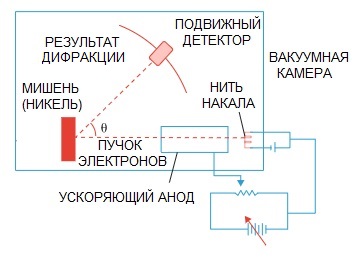
De Broglies hypotes bekräftades senare. Ett fysikexperiment på elektrondiffraktion, utfört 1927 av de amerikanska forskarna Clinton Davison och Lester Germer, påpekade slutligen elektronens vågnatur.

När en elektronstråle riktades genom en speciell atomstruktur verkar det som om detektorn borde ha registrerat bilden som partiklar som flyger efter varandra, vilket logiskt sett skulle förväntas om elektroner var partiklar.

Men i praktiken har vi en bild som är karakteristisk för vågdiffraktion. Dessutom är längderna på dessa vågor helt förenliga med konceptet som de Broglie föreslagit.

I slutändan gjorde de Broglies idé det möjligt att förklara principen för Bohrs atommodell, och senare gjorde det det möjligt för Erwin Schrödinger att generalisera dessa idéer och lägga grunden till modern kvantfysik.