Hur man beräknar induktans
Precis som en kropp med massa i mekanik motstår acceleration i rymden, uppvisande tröghet, så förhindrar induktansen strömmen i en ledare från att förändras, vilket manifesterar självinduktions-EMK. Detta är självinduktionens EMF, som motsätter sig både en minskning av strömmen, försöker behålla den, och en ökning av strömmen, försöker minska den.
Faktum är att i processen att ändra (öka eller minska) strömmen i kretsen ändras också det magnetiska flödet som skapas av denna ström, vilket är lokaliserat huvudsakligen i det område som begränsas av denna krets. Och när det magnetiska flödet ökar eller minskar, inducerar det en EMF av självinduktion (enligt Lenz regel - mot orsaken som orsakar det, det vill säga mot strömmen som nämndes i början), allt i samma krets. Induktansen L här kallas proportionalitetsfaktorn mellan strömmen I och det totala magnetiska flödet Φ, denna ström genereras av:
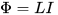
Så ju högre induktans kretsen har, desto starkare är den än det resulterande magnetfältet, det förhindrar strömmen från att förändras (det är fältet som skapar den) och därför kommer det att ta längre tid för strömmen att förändras genom större induktans, med samma pålagda spänning. Följande påstående är också sant: ju högre induktans, desto större blir spänningen över kretsen när det magnetiska flödet genom den ändras.

Antag att vi ändrar det magnetiska flödet i ett visst område med en konstant hastighet, då genom att täcka denna region med olika kretsar, kommer vi att få mer spänning på den kretsen vars induktans är större (transformator, Rumkorf-spole, etc. fungerar enligt denna princip).
Men hur beräknas loopinduktansen? Hur hittar man proportionalitetsfaktorn mellan ström och magnetiskt flöde? Det första att komma ihåg är att induktansen ändras i Henry (H). Vid terminalerna på en krets med en induktans på 1 henry, om strömmen i den ändras med en ampere per sekund, kommer en spänning på 1 volt att visas.
Storleken på induktansen beror på två parametrar: på kretsens geometriska dimensioner (längd, bredd, antal varv etc.) och på mediets magnetiska egenskaper (om det till exempel finns en ferritkärna inuti spole, kommer dess induktans att vara större än om det inte finns någon kärna inuti).
För att beräkna den producerade induktansen är det nödvändigt att veta vilken form själva spolen kommer att ha och vilken magnetisk permeabilitet mediet inuti den kommer att ha (mediets relativa magnetiska permeabilitet är proportionalitetsfaktorn mellan den magnetiska permeabiliteten hos ett vakuum och den magnetiska permeabilitet för ett givet medium.Naturligtvis är det olika för olika material) …
Låt oss titta på formlerna för att beräkna induktansen för de vanligaste formerna av spolar (cylindrisk solenoid, toroid och lång tråd).
Här är formeln för att beräkna induktansen solenoid — spolar vars längd är mycket större än diametern:
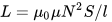
Som du kan se, med att känna till antalet varv N, längden på lindningen l och tvärsnittsarean för spolen S, finner vi den ungefärliga induktansen för spolen utan kärna eller med en kärna, medan den magnetiska vakuumets permeabilitet är ett konstant värde:
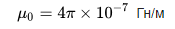
Induktans för en toroidformad spole, där h är toroidens höjd, r är toroidens innerdiameter, R är toroidens yttre diameter:
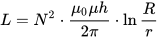
Induktansen för en tunn tråd (radien på tvärsnittet är mycket mindre än längden), där l är längden på tråden och r är radien på dess tvärsnitt. Mu med index i och e är relativ magnetisk permeabilitet för de interna (interna, ledande material) och de externa (externa, material utanför ledaren) miljöer:
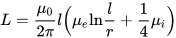
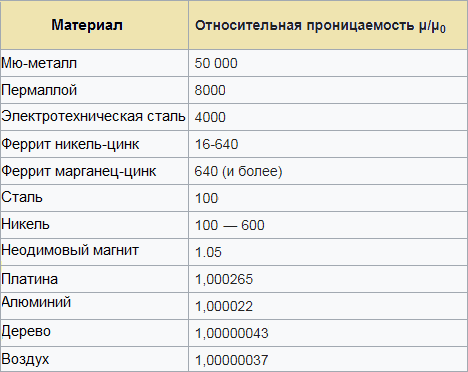
En tabell över relativa permittiviteter hjälper dig att uppskatta vilken induktans du kan förvänta dig från en krets (tråd, spole) som använder ett visst magnetiskt material som kärna: