Trefas nätförsörjning: aktiv, reaktiv, full
Värdena för den totala aktiva och totala reaktiva effekten för trefaskretsen är lika med summan av den aktiva och reaktiva effekten för var och en av de tre faserna A, B respektive C. Detta uttalande illustreras av följande formler:
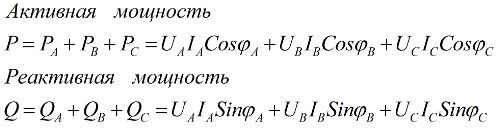
här är Ua, Ub, Uc, Ia, Ib, Ic värdena för fasspänningar och strömmar och φ är fasförskjutningen.
När belastningen är symmetrisk, det vill säga under förhållanden där den aktiva och reaktiva effekten för var och en av faserna är lika med varandra, för att hitta den totala effekten av flerfaskretsen, räcker det att multiplicera värdet på faseffekten med antalet involverade faser. Den totala effekten bestäms baserat på de erhållna värdena för dess aktiva och reaktiva komponenter:
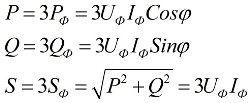
I ovanstående formler kan fasvärdena för kvantiteterna uttryckas i termer av deras linjära värden, som kommer att skilja sig för stjärna eller delta anslutningsscheman för användare, men effektformlerna kommer i slutändan att vara desamma:
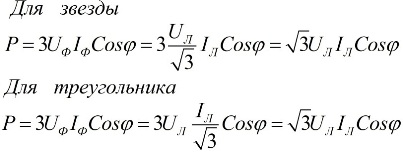
Det följer av ovanstående uttryck att oavsett anslutningsschemat för mottagarna av elektrisk energi, oavsett om det är en triangel eller en stjärna, om belastningen är symmetrisk, kommer formlerna för att hitta kraften att ha samma form, både för en triangel och för en stjärna:
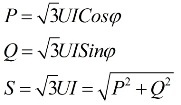
Dessa formler visar linjära värden på spänning och ström och är skrivna utan abonnemang. Vanligtvis hittas en sådan notation, utan subscripts, det vill säga om det inte finns några subscripts, menar vi linjära värden.
En speciell mätanordning, kallad wattmätare… Dess avläsningar bestäms av formeln:
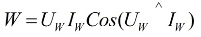
i ovanstående formel är Uw och Iw vektorerna för spänningen som appliceras på lasten och strömmen som flyter genom den.
Typen av den aktiva belastningen och fasanslutningsdiagrammet kan vara olika, därför, beroende på de specifika omständigheterna, kommer anslutningsdiagrammen för wattmätaren att vara olika.
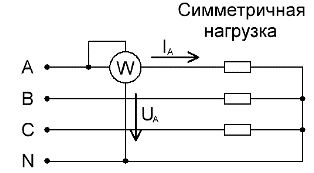
För symmetriskt belastade trefaskretsar, för en grov mätning av den totala aktiva effekten, om hög noggrannhet inte krävs, räcker det med en wattmeter kopplad till endast en av faserna. Efter det, för att få värdet på den aktiva effekten av hela kretsen, återstår det att multiplicera avläsningarna av wattmätaren med antalet faser:
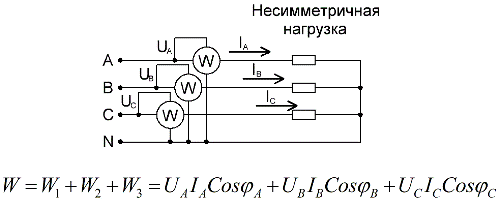
För en fyrtrådskrets med en neutral tråd, för att exakt mäta aktiv effekt, krävs tre wattmätare, som var och en avläses och sedan summeras för att få ett värde för kretsens totala effekt:
Om det inte finns någon neutral ledning i en trefaskrets räcker det med två wattmeter för att mäta den totala effekten, även om belastningen är obalanserad.
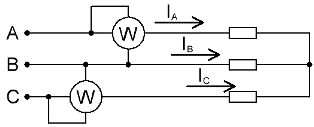
I frånvaro av en neutral ledare är fasströmmarna sammankopplade enligt Kirchhoffs första lag:
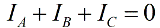
Då blir summan av avläsningarna av ett par wattmätare lika med:
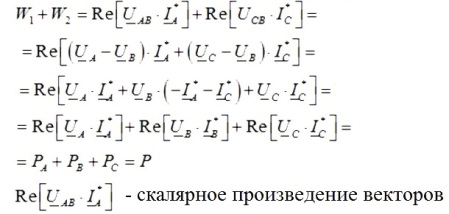
Så, om du lägger till avläsningarna för ett par wattmätare, får du den totala aktiva effekten i den trefaskrets som studeras, och avläsningarna av wattmätarna kommer att bero på både storleken på belastningen och dess natur.
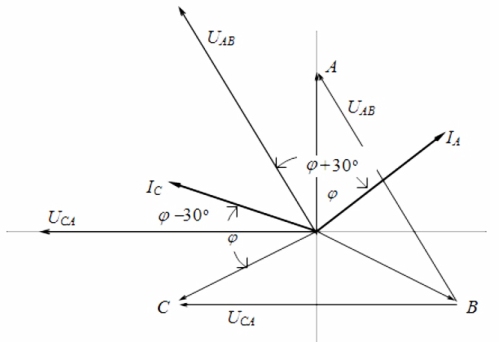
Om man tittar på vektordiagrammet för strömmar och spänningar i samband med en symmetrisk belastning kan man dra slutsatsen att avläsningarna av wattmätare bestäms av följande formler:
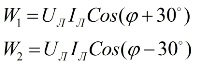
Efter att ha analyserat dessa uttryck kan det förstås att med en rent aktiv belastning, när φ = 0, kommer avläsningarna för de två wattmetrarna att vara lika med varandra, det vill säga W1 = W2.
Med aktiv belastningsinduktans, när 0 ≤ φ ≤ 90 °, kommer avläsningarna för wattmeter 1 att vara mindre än de för wattmeter 2, det vill säga W1 60 °, avläsningarna för wattmeter 1 kommer att vara negativa, det vill säga W1 <0.
Med en aktiv kapacitiv karaktär av belastningen, när 0 ≥ φ≥ -90 °, kommer avläsningarna av wattmätaren 2 att vara mindre än wattmätaren 1, det vill säga W1> W2. Vid φ <-60 ° blir avläsningarna för wattmätaren 2 negativa.
