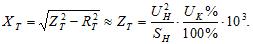Reservkretsar för transformatorer vid beräkning av elektriska nätverk

Av karaktären på de uppgifter som ska lösas är beräkningarna av elektriska nätverk uppdelade i två delar:

1. Beräkningar av nätverkslägen. Det är beräkningar av spänningar i nodpunkter, strömmar och effekter i ledningar och transformatorer vid vissa intervall.

2. Parametervalsberäkningar. Dessa är beräkningar av valet av spänningar, parametrar för linjer, transformatorer, kompensering och andra enheter.

För att göra ovanstående beräkningar måste du först känna till ekvivalenta kretsar, motstånd och konduktans för kraftledningar och transformatorer.

Vid beräkningar av elektriska nätverk, med hänsyn till transformatorer, används vanligtvis den enklaste L-formade ekvivalenta kretsen istället för den T-formade ekvivalenta kretsen som är känd från elteknik, vilket avsevärt förenklar beräkningarna och inte orsakar betydande fel . En sådan ekvivalent krets visas i fig. 1.

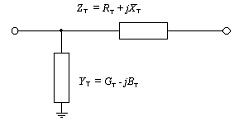
Ris. 1. L-formad transformator ekvivalent krets

Huvudparametrarna för den ekvivalenta kretsen för en fas av transformatorn är det aktiva motståndet RT, reaktivitet HT, aktiv konduktans GT och reaktiv konduktans BT. Den reaktiva konduktansen hos VT är induktiv till sin natur. Dessa parametrar saknas i referenslitteraturen. De bestäms experimentellt enligt passdata: tomgångsförluster ∆PX, kortslutningsförluster DRK, kortslutningsspänning UK% och tomgångsström i0%.

För transformatorer med tre lindningar eller autotransformatorer presenteras motsvarande krets i en något annorlunda form (fig. 2).

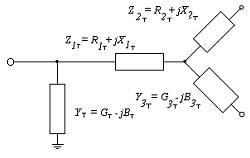
Ris. 2. Ekvivalent krets för en transformator med tre lindningar

I passdata för transformatorer med tre lindningar indikeras kortslutningsspänningen för tre möjliga kombinationer: UK1-2%-kortslutning på mellanspänningslindningen (MV) och matningssidan av högspänningslindningen (HV). ; UK1-3% — vid kortslutning av lågspänningslindningen (LV) och strömförsörjningen från HV-lindningen; UK2-3% — vid kortslutning av LV-spolen och matningen på HV-sidan.

Dessutom är versioner av transformatorn möjliga när alla tre lindningarna är konstruerade för transformatorns märkeffekt eller när en eller båda sekundärlindningarna är konstruerade (i termer av uppvärmning) för endast 67 % av primärlindningens effekt.

Den aktiva och reaktiva ledningsförmågan för den ekvivalenta kretsen bestäms av formlerna:

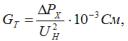
där ∆PX — i kW, UN — i kW.

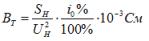
Det totala aktiva motståndet för lindningarna RTotot beräknas med formeln:

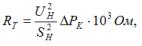
Om alla tre lindningarna är designade för full effekt, tas det aktiva motståndet för var och en av dem lika:

R1T = R2T = R3T = 0,5 RT totalt

Om en av sekundärlindningarna är konstruerad för 67% av effekten, tas resistanserna hos lindningarna som kan belastas med 100% lika med 0,5 RTotal. En spole som tillåter överföring av 67 % av effekten och vars tvärsnitt är 67 % av det normala har ett motstånd 1,5 gånger mer, d.v.s. 0,75 RTotot.

För att bestämma resistansen för var och en av strålarna presenteras de ekvivalenta kretsarna för kortslutningsspänningen som summan av de relativa spänningsfallen på de individuella strålarna:

UK1-2% = UK1% + UK2%,

UK1-3% = UK1% + UK3%,

UK2-3% = UK2% + UK3%.

När vi löser detta ekvationssystem för UK1% och UK3% får vi:

UK1% = 0,5 (UK1-2% + UK1-3%-UK2-3%),

UK2% = UK1-2% + UK1%,

UK3% = UK1-3% + UK1%.

I praktiska beräkningar för en av strålarna är spänningsfallet vanligtvis noll eller ett litet negativt värde. För denna stråle av den ekvivalenta kretsen antas det induktiva motståndet vara noll, och för de återstående strålarna hittas de induktiva reaktanserna beroende på de relativa spänningsfallen med formeln: