Öka effektfaktorn i sinusformade strömkretsar

De flesta moderna konsumenter av elektrisk energi har en induktiv karaktär av lasten, vars strömmar ligger efter källspänningen. Så för induktionsmotorer, transformatorer, svetsmaskiner och annan reaktiv ström behövs för att skapa ett roterande magnetfält i elektriska maskiner och ett alternerande magnetiskt flöde i transformatorer.

Den aktiva effekten hos sådana konsumenter vid de givna värdena för ström och spänning beror på cosφ:

P = UICosφ, I = P/UCosφ

En minskning av effektfaktorn leder till en ökning av strömmen.

Cosinus phi den reduceras särskilt kraftigt när motorer och transformatorer går på tomgång eller är under tung belastning. Om nätet har reaktiv ström utnyttjas inte kraften från generatorn, transformatorstationerna och nätverken fullt ut. När cosφ minskar ökar de avsevärt förlust av energi för uppvärmning av ledningar och spolar av elektriska apparater.

Till exempel, om den verkliga effekten förblir konstant, förses den med en ström på 100 A vid cosφ= 1, sedan med minskande cosφ till 0,8 och samma effekt, ökar strömmen i nätverket med 1,25 gånger (I = Inetwork x cosφ , Azac = Aza/cosφ).

Förluster på värmenätets ledningar och lindningar av en generator (transformator) Pload = I2nets x Rnets är proportionella mot kvadraten på strömmen, det vill säga de ökar med 1,252 = 1,56 gånger.

Vid cosφ= 0,5 är strömmen i nätverket med samma aktiva effekt lika med 100 / 0,5 = 200 A, och förlusterna i nätverket ökar med 4 gånger (!). Det växer nätspänningsförlustersom stör andra användares normala funktion.

Användarens mätare rapporterar i alla fall samma mängd förbrukad aktiv energi per tidsenhet, men i det andra fallet matar generatorn nätet med en ström som är 2 gånger större än den i det första. Generatorbelastningen (termiskt läge) bestäms inte av konsumenternas aktiva effekt, utan av den totala effekten i kilovolt-ampere, det vill säga produkten av spänningen av strömstyrkaflyter genom spolarna.

Om vi ​​betecknar motståndet hos trådarna i linjen Rl, kan effektförlusten i den bestämmas enligt följande:

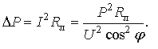
Därför, ju större användaren är, desto mindre effektförluster i ledningen och desto billigare överföring av el.

Effektfaktorn visar hur källans märkeffekt används. Så för att förse mottagaren med 1000 kW vid φ= 0,5 bör generatoreffekten vara S = P / cosφ = 1000 / 0,5 = 2000 kVA, och vid cosφ = 1 C = 1000 kVA.

En ökning av effektfaktorn ökar därför kraftutnyttjandet av generatorerna.

För att öka effektfaktorn (cosφ) används elektriska installationer reaktiv effektkompensation.

Att öka effektfaktorn (minska vinkeln φ — fasförskjutning av ström och spänning) kan uppnås på följande sätt:

1) byte av lätt belastade motorer med motorer med lägre effekt,

2) under spänning

3) frånkoppling av tomgångsmotorer och transformatorer,

4) införandet av speciella kompensationsanordningar i nätverket, som är generatorer av den ledande (kapacitiva) strömmen.

För detta ändamål är synkrona kompensatorer - synkrona överexciterade elmotorer - speciellt installerade vid kraftfulla regionala transformatorstationer.

Synkrona kompensatorer

För att öka effektiviteten hos kraftverk är de vanligaste kondensatorbankerna kopplade parallellt med den induktiva lasten (fig. 2 a).

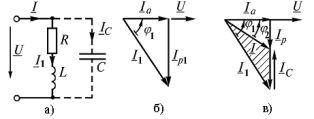
Ris. 2 Slå på kondensatorer för reaktiv effektkompensation: a — krets, b, c — vektordiagram

För att kompensera cosφ i elektriska installationer upp till flera hundra kVA används de cosinus kondensatorer… De produceras för spänningar från 0,22 till 10 kV.

Kapaciteten hos kondensatorn som krävs för att öka cosφ från det befintliga värdet cosφ1 till den nödvändiga cosφ2 kan bestämmas från diagrammet (fig. 2 b, c).

När ett vektordiagram konstrueras tas källspänningsvektorn som den initiala vektorn. Om belastningen är induktiv, släpar strömvektorn Az1 efter vinkeln för spänningsvektorn φ1Aza sammanfaller i riktning med spänningen, den reaktiva komponenten av strömmen Azp släpar efter den med 90 ° (Fig. 2 b).

Efter anslutning av kondensatorbanken till användaren bestäms strömmen Az som en geometrisk summa av vektorerna Az1 och Az° C... I detta fall föregår den kapacitiva strömvektorn spänningsvektorn med 90 ° (fig. 2, c). . Detta visar vektordiagrammet φ2 <φ1, dvs. efter påslagning av kondensatorn ökar effektfaktorn från cosφ1 till cosφ2

Kapaciteten hos en kondensator kan beräknas med hjälp av ett vektordiagram av strömmar (fig. 2 c) Ic = azp1 — Azr = Aza tgφ1 — Aza tgφ2 = ωCU

Med tanke på att P = UI, skriver vi kapacitansen för kondensatorn C = (I / ωU) NS (tgφ1 — tgφ2) = (P / ωU2) NS (tgφ1 — tgφ2).

I praktiken ökas effektfaktorn vanligtvis inte till 1,0, utan till 0,90 - 0,95, eftersom full kompensation kräver ytterligare installation av kondensatorer, vilket ofta inte är ekonomiskt motiverat.