Hur är DC-mätbryggor arrangerade och manövrerade?

Enheten för enstaka mätbryggor av likström

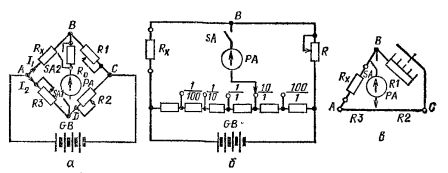
En enda likström består av tre provmotstånd (vanligtvis justerbara) R1, R2, R3 (Fig. 1, a), som är kopplade i serie med det uppmätta motståndet Rx i bryggkretsen.

Ström tillförs en av diagonalerna i denna krets från EMF-källan GB, och en mycket känslig galvanometer RA är ansluten till den andra diagonalen genom omkopplaren SA1 och begränsningsresistansen Ro.

Ris. 1. Schema för enstaka likströmsmätbryggor: a — Allmänt; b — med en jämn förändring i armförhållandet och en skarp förändring i jämförelsearmen.

Schemat fungerar enligt följande. När ström tillförs genom motstånden Rx, Rl, R2, R3, strömmarna I1 och I2... Dessa strömmar kommer att orsaka ett spänningsfall över motstånden Uab, Ubc, Uad och Udc.

Om dessa spänningsfall är olika, kommer potentialerna vid punkterna φa, φb och φc inte att vara desamma.Därför, om du slår på galvanometern med omkopplaren SA1, då är en ström lika med Azr = (φb — φd) / Po.

Mätarens uppgift är att balansera bryggan, det vill säga att göra potentialerna för punkterna φb och φd lika, med andra ord minska galvanometerströmmen till noll.

För att göra detta börjar de ändra motstånden för motstånden R1, R2 och R3 tills galvanometerströmmen blir noll.

Vid Azr = 0 kan man hävda att φb = φd... Detta är endast möjligt när spänningen sjunker Uab — Uad och typ BC. = Udc.

Genom att ersätta dessa uttryck med spänningsfallsvärdena Uad =I2R3, Ubc = I1R1, Udc = I2R2 och Uab = I1Rx, vi får två likheter: I1Rx = I2R3, I1R1 = I2R2

Om vi ​​dividerar den första likheten med den andra får vi RHC / R1 = R3 / R2 eller RNS R2 = R1 R3

Den sista jämlikheten är balanseringsvillkoret för en enkelbrygga DC.

Det följer att bron är balanserad när produkterna av motstånden från de motsatta armarna är lika. Därför bestäms det uppmätta motståndet av formeln Rx = R1R3 / R2

I verkliga enhetsbryggor, antingen motståndet hos motståndet R1 (kallad komparatorarm) eller förhållandet mellan motstånden R3/R2.

Det finns mätbryggor där endast referensarmens motstånd ändras och förhållandet R3/R2 förblir konstant. Omvänt ändras endast förhållandet R3 / R2, medan jämförelsearmens motstånd förblir konstant.

De mest utbredda är mätbryggorna, där motståndet R1 ändras smidigt och med hopp, vanligtvis multiplar av 10, ändras förhållandet R3 / R2 (fig. 1, b), till exempel i de vanliga mätbryggorna P333.

Ris. 2.Likströmsmätbrygga P333

Varje mätbrygga kännetecknas av ett resistansmätområde från Rmin till Rmax. En viktig parameter för bron är dess känslighet. Sm = SGСcx, där Sg =da /dIg är galvanometerns känslighet, Scx =dIG/dR - kretsens känslighet.

Genom att ersätta Sg och Scx i Sm får vi Sm = da/dR.

Ibland används begreppet mätbryggans relativa känslighet:

Cm= da/ (dR/R).

där dR / R — den relativa förändringen i motståndet i den uppmätta armen, da — avböjningsvinkeln för galvanometernålen.

Beroende på konstruktionen skiljer man mellan stock- och linjära (rekord)mätbryggor.

I den butiksbaserade mätbryggan görs armmotstånden i form av en plugg eller spak, flervärdiga mått på elektriskt motstånd (motstånd), i rekordbroar är jämförelsearmen gjord i form av ett butiksmotstånd, och avböjningsarmarna är i form av ett motstånd, separerade av en glidare i två justerbara delar.

Tillåtet fel, enstaka mätbryggor av likström har en noggrannhetsklass: 0,02; 0,05; 0,1; 0,2; 1,0; 5.0. Noggrannhetsklassens numeriska värde motsvarar det största tillåtna värdet på det relativa felet.

Felet för en enstaka DC-brygga beror på graden av jämförbarhet av resistanserna hos anslutningstrådarna och kontakter med det uppmätta motståndet. Ju mindre uppmätt motstånd, desto större fel. Därför används dubbla DC-bryggor för att mäta lågt motstånd.

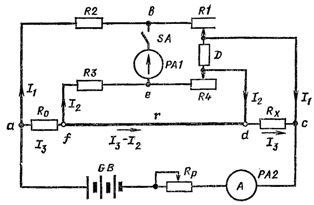
DC dubbelbrygga enhet

Armarna på den dubbla (sexarmade) mätbryggan är det uppmätta motståndet Rx (de är gjorda med fyra klämmor för att minska påverkan av kontaktresistanser och är anslutna till nätverket med en speciell enhet med fyra klämmor), ett exempelmotstånd Ro och två par hjälpmotstånd Rl, R2, R3, R4.

Ris. 3 Schematisk beskrivning av en dubbel mätande DC-brygga

Balansen på bron bestäms av formeln:

Rx = Ro NS (R1 / R2) — (r R3 / (r + R3 + R4)) NS (R1 / R2 — R4 / R3)

Detta visar att om två armförhållanden R1 / R2 och R4 / R3 är lika med varandra, så är det subtraherade noll.

Trots det faktum att motstånden R1 och R4 som flyttar skjutreglaget D är inställda på samma sätt, på grund av spridningen av parametrarna för motstånden R2 och R4, är detta mycket svårt att uppnå.

För att minska mätfelet bör resistansen hos bygeln som ansluter referensmotståndet Ro och den uppmätta resistansen Rx tas så liten som möjligt. Ett speciellt kalibrerat motstånd är vanligtvis anslutet till enheten. r... Då blir det subtraherade uttrycket praktiskt taget noll.

Värdet på det uppmätta motståndet kan bestämmas med formeln: Rx = Ro R1/R2

Dubbla DC-doseringsbryggor är utformade för att endast fungera med variabla armförhållanden. Dubbelbryggans känslighet beror på nollpekarens känslighet, bryggkretsens parametrar och värdet på driftströmmen. När driftströmmen ökar, ökar känsligheten.

De vanligaste är kombinerade DC-mätbryggor utformade för att fungera på enkel- och dubbelbryggsystem.