Förluster och spänningsfall - vad är skillnaderna

I vanligt mänskligt liv används orden "förlust" och "fall" för att beteckna faktumet av en minskning av vissa prestationer, men de betyder ett annat värde.

I detta fall betyder "förluster" förlust av en del, skada, minskning av storleken på den tidigare uppnådda nivån. Förluster är oönskade, men du kan tolerera dem.

Ordet "falla" förstås som en allvarligare skada förknippad med ett fullständigt fråntagande av rättigheter. Således kan även enstaka förluster (säg en portfölj) över tid leda till en nedgång (till exempel nivån på den materiella livslängden).

I detta avseende kommer vi att överväga denna fråga i förhållande till spänningen i det elektriska nätverket.

Hur förluster och spänningsfall bildas

Elektricitet transporteras över långa avstånd med luftledningar från en transformatorstation till en annan.

Luftledningar är utformade för att överföra den tillåtna kraften och är gjorda av metalltrådar av ett visst material och sektion. De skapar en resistiv belastning med ett motståndsvärde på R och en reaktiv belastning på X.

På den mottagande sidan står den transformatorelkonvertering.Dess spolar har ett aktivt och uttalat induktivt motstånd XL. Transformatorns sekundära sida sänker spänningen och överför den vidare till konsumenterna, vars belastning uttrycks av värdet på Z och är aktiv, kapacitiv och induktiv till sin natur. Detta påverkar också nätverkets elektriska parametrar.

Spänningen som appliceras på ledningarna till luftledningens stöd, närmast kraftöverföringsstationen, övervinner kretsens reaktiva och aktiva motstånd i varje fas och skapar en ström i den, vars vektor avviker från vektorn för kretsen. pålagd spänning med en vinkel φ.

Typen av fördelningen av spänningar och flödet av strömmar längs linjen för ett symmetriskt belastningsläge visas på bilden.

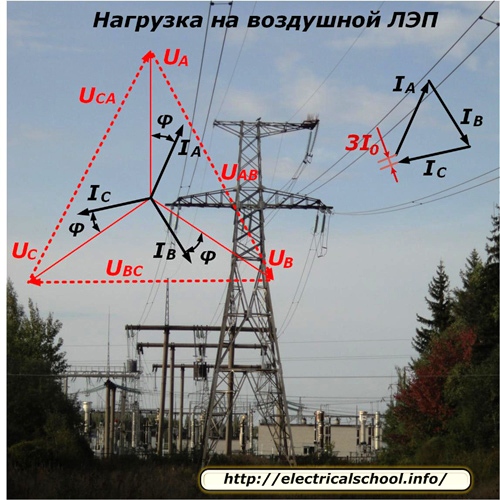
Eftersom varje fas av linjen matar ett annat antal konsumenter som också är slumpmässigt frånkopplade eller anslutna till arbetet, är det tekniskt mycket svårt att perfekt balansera fasbelastningen. Det finns alltid en obalans i den, som bestäms av vektortillägget av fasströmmarna och skrivs som 3I0. I de flesta beräkningar ignoreras det helt enkelt.

Energin som förbrukas av den sändande transformatorstationen används delvis för att övervinna ledningens motstånd och når den mottagande sidan med liten förändring. Denna fraktion kännetecknas av förlust och spänningsfall, vars vektor minskar något i amplitud och förskjuts med en vinkel i varje fas.

Hur förluster och spänningsfall beräknas

För att förstå de processer som äger rum under överföringen av elektricitet är vektorformen lämplig för att representera huvudegenskaperna. Olika matematiska beräkningsmetoder bygger också på denna metod.

För att förenkla beräkningarna i trefassystem den representeras av tre enfas ekvivalenta kretsar. Denna metod fungerar bra med en symmetrisk belastning och låter dig analysera processerna när den är trasig.

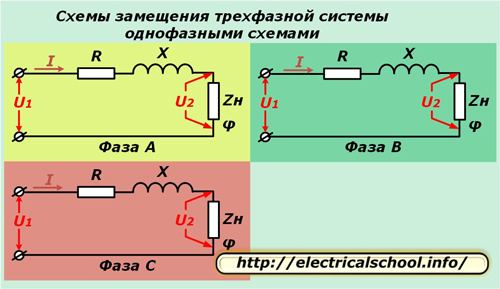
I diagrammen ovan är den aktiva R och reaktansen X för varje ledare i linjen anslutna i serie med det komplexa belastningsmotståndet Zn som kännetecknas av vinkeln φ.

Dessutom utförs beräkning av spänningsförlust och spänningsfall i en fas. För att göra detta måste du ange data. För detta ändamål väljs en transformatorstation som tar emot energi, där den tillåtna belastningen redan måste fastställas.

Spänningsvärdet för alla högspänningssystem anges redan i referensböckerna, och ledningarnas resistanser bestäms av deras längd, tvärsnitt, material och nätverkskonfiguration. Den maximala strömmen i kretsen är inställd och begränsad av ledningarnas egenskaper.

För att starta beräkningarna har vi därför: U2, R, X, Z, I, φ.

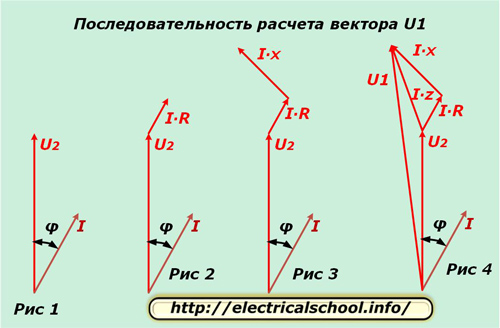
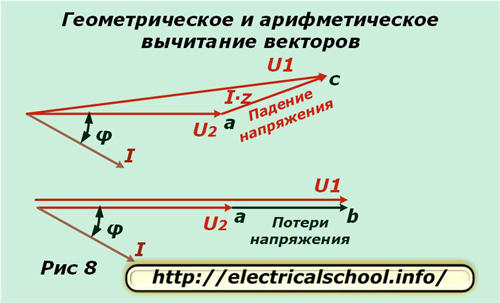
Vi tar en fas, till exempel «A» och separerar för den i det komplexa planet vektorerna U2 och I, förskjutna med en vinkel φ, som visas i figur 1. Potentialskillnaden i ledarens aktiva motstånd sammanfaller i riktning med strömmen och i magnitud bestäms från uttrycket I ∙ R. Vi skjuter upp denna vektor från slutet av U2 (fig. 2).

Potentialskillnaden i ledarens reaktans skiljer sig från strömriktningen med en vinkel φ1 och beräknas från produkten I ∙ X. Vi skjuter upp den från vektorn I ∙ R (fig. 3).

Påminnelser: för den positiva rotationsriktningen för vektorerna i det komplexa planet tas motursrörelsen. Strömmen som flyter genom den induktiva lasten släpar efter den pålagda spänningen med en vinkel.

Figur 4 visar plottningen av potentialskillnadsvektorerna på den totala trådresistansen I ∙ Z och spänningen vid ingången till kretsen U1.

Nu kan du jämföra ingångsvektorerna med motsvarande krets och över lasten. För att göra detta, lägg det resulterande diagrammet horisontellt (fig. 5) och rita en båge från början med radien för modulen U1 tills den skär med riktningen för vektorn U2 (fig. 6).

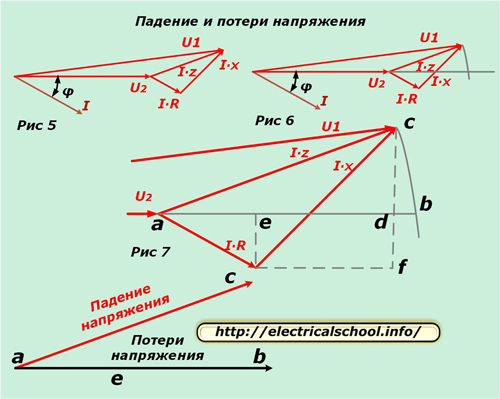
Figur 7 visar en förstoring av triangeln för större klarhet och ritning av hjälplinjer, som indikerar de karakteristiska skärningspunkterna med bokstäver.

Längst ner på bilden visas att den resulterande vektorn ac kallas spänningsfallet och ab kallas förlusten. De skiljer sig åt i storlek och riktning. Om vi ​​återgår till den ursprungliga skalan kommer vi att se att ac erhålls som ett resultat av geometrisk subtraktion av vektorer (U2 från U1), och ab är aritmetisk. Denna process visas på bilden nedan (fig. 8).

Härledning av formler för beräkning av spänningsförluster

Låt oss nu gå tillbaka till figur 7 och lägga märke till att bd-segmentet är mycket litet. Av denna anledning försummas det i beräkningarna och spänningsförlusten beräknas från segmentlängden ad. Den består av två linjesegment ae och ed.

Eftersom ae = I ∙ R ∙ cosφ och ed = I ∙ x ∙ sinφ, kan spänningsförlust för en fas beräknas med formeln:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

Om vi ​​antar att belastningen är symmetrisk i alla faser (villkorligt försummar 3I0), kan vi använda matematiska metoder för att beräkna spänningsförlusten i ledningen.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Om den högra sidan av denna formel multipliceras och divideras med nätverksspänningen Un, så får vi en formel som gör att vi kan utföra pBeräkning av spänningsförluster genom strömförsörjningen.

∆Ul = (P ∙ r + Q ∙ x) / Un

Värdena för aktiv P och reaktiv Q-effekt kan hämtas från linjemätaravläsningar.

Sålunda beror spänningsförlusten i en elektrisk krets på:

• aktiv och reaktans hos kretsen;

• komponenter av applicerad kraft;

• storleken på den applicerade spänningen.

Härledning av formler för beräkning av den tvärgående komponenten av spänningsfallet

Låt oss gå tillbaka till figur 7. Värdet på vektorn ac kan representeras av hypotenusan av en rätvinklig triangel acd. Vi har redan beräknat annonsfoten. Låt oss bestämma den tvärgående komponenten cd.

Figuren visar att cd = cf-df.

df = ce = I ∙ R ∙ sin φ.

cf = I ∙ x ∙ cos φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

Med hjälp av de erhållna modellerna utför vi små matematiska transformationer och erhåller den tvärgående komponenten av spänningsfallet.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Bestämning av formeln för beräkning av spänningen U1 i början av kraftledningen

Genom att känna till värdet på spänningen i slutet av linjen U2, förlusten ∆Ul och den tvärgående komponenten av droppen δU, kan vi beräkna värdet på vektorn U1 genom Pythagoras sats. I utökad form har den följande form.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Praktisk användning

Beräkningen av spänningsförluster utförs av ingenjörer vid skapandet av ett elektriskt kretsprojekt för det optimala valet av nätverkets konfiguration och dess beståndsdelar.

Under driften av elektriska installationer kan vid behov samtidiga mätningar av spänningsvektorerna vid ändarna av ledningarna utföras periodiskt och resultaten som erhålls med metoden för enkla beräkningar kan jämföras. Denna metod är lämplig för enheter som har ökat krav på grund av behovet av hög arbetsnoggrannhet.

Spänningsförluster i sekundära kretsar

Ett exempel är sekundärkretsarna för mätspänningstransformatorer, som ibland når flera hundra meter i längd och överförs av en speciell strömkabel med ökat tvärsnitt.

De elektriska egenskaperna hos en sådan kabel är föremål för ökade krav på kvaliteten på spänningsöverföring.

Modernt skydd av elektrisk utrustning kräver drift av mätsystem med höga metrologiska indikatorer och en noggrannhetsklass på 0,5 eller till och med 0,2. Därför måste förluster av spänningen som appliceras på dem övervakas och beaktas. Annars kan felet som introduceras av dem i driften av utrustningen avsevärt påverka alla driftsegenskaper.

Spänningsförluster i långa kabellinjer

Egenskapen med utformningen av den långa kabeln är att den har ett kapacitivt motstånd på grund av det ganska nära arrangemanget av ledande kärnor och ett tunt lager av isolering mellan dem. Den avleder ytterligare strömvektorn som passerar genom kabeln och ändrar dess storlek.

Effekten av spänningsfall på kapacitiv resistans måste beaktas i beräkningen för att ändra värdet på I ∙ z. Annars förändras inte tekniken som beskrivs ovan.

Artikeln ger exempel på förluster och spänningsfall på luftledningar och kablar. De finns dock hos alla konsumenter av el, inklusive elmotorer, transformatorer, induktorer, kondensatorbanker och andra enheter.

Mängden spänningsförluster för varje typ av elektrisk utrustning är lagligt reglerad när det gäller driftsförhållanden, och principen för deras bestämning i alla elektriska kretsar är densamma.