Vad är spänningsbortfall och orsakerna till spänningsbortfall

Förlust av nätspänning

För att förstå vad spänningsförlust är, överväg spänningsvektordiagrammet för en trefas växelströmsledning (fig. 1) med en enda belastning i slutet av linjen (fig. 1)I).

Antag att den aktuella vektorn bryts upp i komponenterna Azi och AzP. I fig. 2 är fasspänningsvektorerna i slutet av linjen ritade i skala U3ph och strömmen AziLing i fas med en vinkel φ2.

För att få spänningsvektorn i början av linjen U1φ följer vektorn i slutet U2ph, rita linjespänningsfallstriangeln (abc) på spänningsskalan. För detta är vektorn ab, lika med produkten av ström och aktiv resistans för linjen (AzR), placerad parallellt med strömmen, och vektorn b° C, lika med produkten av ström och induktiv resistans hos linjen ( AzX), är vinkelrät mot den aktuella vektorn .Under dessa förhållanden motsvarar den räta linjen som förbinder punkterna O och c storleken och positionen i rymden av spänningsvektorn i början av linjen (U1e) i förhållande till spänningsvektorn i slutet av linjen (U2e). Genom att ansluta ändarna av vektorerna U1f och U2e får vi spänningsfallsvektorn för den linjära impedansen ac = IZ.

Ris. 1. Schematiskt med en enda ändbelastning

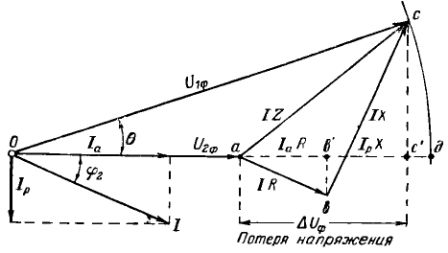
Ris. 2. Vektordiagram över spänningar för en linje med en enda last. Förlust av nätspänning.

Gå med på att kalla spänningsförlust den algebraiska skillnaden mellan fasspänningarna i början och slutet av linjen, det vill säga segment ad eller nästan lika segment ac '.

Vektordiagrammet och relationerna som härrör från det visar att spänningsförlusten beror på nätverkets parametrar, såväl som på de aktiva och reaktiva komponenterna i strömmen eller lasten.

Vid beräkning av mängden spänningsbortfall i nätet ska alltid det aktiva motståndet beaktas, och det induktiva motståndet kan försummas i belysningsnät och i nät gjorda med tvärsnitt upp till 6 mm2 och kablar upp till 35 mm2.

Bestämning av spänningsförlust i nätet

Spänningsförlusten för ett trefassystem anges vanligtvis för linjära storheter, som bestäms av formeln

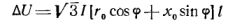
där l — längden på motsvarande sektion av nätet, km.

Om vi ​​ersätter ström med effekt kommer formeln att ha formen:

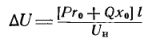
där P. — aktiv effekt, B- reaktiv effekt, kVar; l — sträckans längd, km; Un — nominell nätspänning, kV.

Ändring av nätspänning

Tillåtet spänningsfall

För varje effektmottagare, en viss spänningsförlust... Till exempel har induktionsmotorer en spänningstolerans på ± 5% under normala förhållanden.Detta betyder att om den nominella spänningen för denna elmotor är 380 V, så bör spänningen U„extra = 1,05 Un = 380 x1,05 = 399 V och U»add = 0,95 Un = 380 x 0,95 = 361 V betraktas som högsta tillåtna spänningsvärden. Naturligtvis kommer alla mellanspänningar mellan värdena 361 och 399 V också att tillfredsställa användaren och utgöra en viss zon som kan kallas zonen med önskade spänningar.

Eftersom det under företagets drift sker en konstant förändring av belastningen (kraft eller ström som flyter genom ledningarna vid en viss tid på dagen), kommer olika spänningsförluster att uppstå i nätverket, varierande från de högsta motsvarande värdena till maximalt belastningsläge dUmax, till det minsta dUmin som motsvarar användarens minsta belastning.

För att beräkna mängden av dessa spänningsförluster, använd formeln:

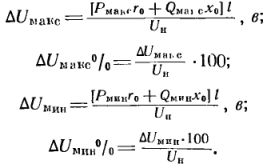
Av vektordiagrammet för spänningar (fig. 2) följer att den faktiska spänningen för mottagaren U2f kan erhållas om vi subtraherar värdet dUf från spänningen i början av linjen U1f, eller, byter till en linjär, dvs. fas -till-fas spänning får vi U2 = U1 — dU

Beräkning av spänningsförluster

Ett exempel. Konsumenten, som består av asynkronmotorer, är ansluten till bussarna till företagets transformatorstation, som upprätthåller en konstant spänning under hela dagen U1 = 400 V.

Den högsta användarbelastningen noteras kl. 11, medan spänningsförlusten dUmax = 57 V, eller dUmax% = 15%. Den minsta konsumentbelastningen motsvarar lunchrasten, medan dUmin — 15,2 V, eller dUmin% = 4%.

Det är nödvändigt att bestämma den faktiska spänningen hos användaren i högsta och lägsta belastningsläge och kontrollera att den ligger inom det önskade spänningsområdet.

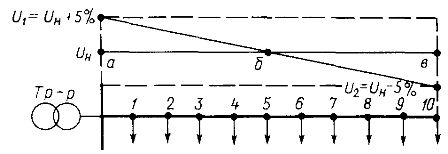
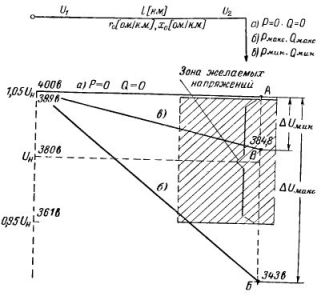Ris. 3. Potentialdiagram för en linje med en enkel belastning för att bestämma spänningsförlusten

Svar. Bestäm de faktiska spänningsvärdena:

U2Max = U1 — dUmax = 400 — 57 = 343 V

U2min = U1 — dUmin = 400 — 15,2 = 384,8V

Den önskade spänningen för asynkronmotorer med Un = 380 V måste uppfylla villkoret:

399 ≥ U2zhel ≥ 361

Genom att ersätta de beräknade spänningsvärdena med olikheten ser vi till att för det största belastningsläget inte är uppfyllt förhållandet 399> 343> 361, och för de minsta belastningarna 399> 384,8> 361 är uppfyllt.

Utgång. I läget med största belastningar är spänningsförlusten så stor att spänningen hos användaren går ut ur zonen för de önskade spänningarna (minska) och inte tillfredsställer användaren.

Detta exempel kan illustreras grafiskt med potentialdiagrammet i fig. 3. I frånvaro av ström kommer spänningen hos användaren att vara numeriskt lika med matningsbussarnas spänning. Eftersom spänningsfallet är proportionellt mot matningsledningens längd, ändras spänningen i närvaro av en last längs linjen i en lutande rät linje från värdet U1 = 400 V till värdet U2Max = 343 V och U2min = 384,8 V .

Som framgår av diagrammet har spänningen vid den högsta belastningen lämnat zonen med önskade spänningar (punkt B på grafen).

Sålunda, även med en konstant spänning på matningstransformatorns samlingsskenor, kan plötsliga förändringar i belastningen skapa ett oacceptabelt spänningsvärde på mottagaren.

Dessutom kan det hända att när belastningen på nätet ändras från den högsta belastningen under dagen till den lägsta belastningen på natten, kommer själva kraftsystemet inte att kunna tillhandahålla den nödvändiga spänningen vid transformatorterminalerna. I båda fallen måste man tillgripa lokal, huvudsakligen spänningsförändring.

Spänningsbortfall i transformatorn (i bilder)