Spänningsresonans
Om AC-kretsen är seriekopplad induktor och kondensator, då påverkar de på sitt sätt generatorn som matar kretsen och fasanslutningarna mellan ström och spänning.
En induktor introducerar en fasförskjutning där strömmen släpar efter spänningen med en fjärdedel av en period, medan en kondensator tvärtom gör att spänningen i kretsen släpar efter strömmen med en fjärdedel av en period. Således är effekten av induktivt motstånd på fasförskjutningen mellan ström och spänning i en krets motsatt effekten av kapacitiv resistans.
Detta leder till att den totala fasförskjutningen mellan ström och spänning i kretsen beror på förhållandet mellan de induktiva och kapacitiva resistansvärdena.
Om värdet på kretsens kapacitiva resistans är större än den induktiva, är kretsen kapacitiv till sin natur, det vill säga spänningen ligger efter strömmen i fas. Om tvärtom kretsens induktiva resistans är större än den kapacitiva, så leder spänningen strömmen och därför är kretsen induktiv.
Den totala reaktansen Xtot för kretsen vi överväger bestäms genom att addera det induktiva motståndet för spolen XL och det kapacitiva motståndet för kondensatorn XC.
Men eftersom verkan av dessa motstånd i kretsen är motsatt, tilldelas en av dem, nämligen Xc, ett minustecken, och den totala reaktansen bestäms av formeln:
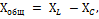
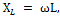
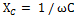
Applicera på denna krets Ohms lag, vi får:
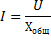
Denna formel kan omvandlas enligt följande:
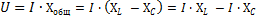
I den resulterande ekvationen, AzxL - det effektiva värdet av komponenten av kretsens totala spänning, som kommer att övervinna kretsens induktiva resistans, och AzNSC - det effektiva värdet av komponenten av kretsens totala spänning, vilket kommer att övervinna det kapacitiva motståndet.
Således kan den totala spänningen för en krets som består av en seriekoppling av en spole och en kondensator betraktas som bestående av två termer, vars värden beror på värdena för den induktiva och kapacitiva resistansen hos krets.
Vi trodde att en sådan krets inte har något aktivt motstånd. Men i de fall där kretsens aktiva resistans inte längre är så liten att den är försumbar, bestäms kretsens totala resistans av följande formel:
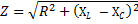
där R är kretsens totala aktiva resistans, XL -NSC — dess totala reaktans. När vi går till formeln för Ohms lag har vi rätt att skriva:
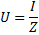
AC spänningsresonans
Induktiva och kapacitiva resistanser kopplade i serie orsakar mindre fasförskjutning mellan ström och spänning i en växelströmskrets än om de ingick i kretsen separat.
Med andra ord, från den samtidiga verkan av dessa två reaktioner av olika karaktär i kretsen sker kompensation (ömsesidig förstörelse) av fasförskjutningen.
Full ersättning, dvs. fullständig eliminering av fasförskjutningen mellan ström och spänning i en sådan krets kommer att inträffa när det induktiva motståndet är lika med kretsens kapacitiva resistans, dvs när XL = XC eller, vilket är detsamma, när ωL = 1 / ωC.
I det här fallet kommer kretsen att bete sig som ett rent aktivt motstånd, det vill säga som om den varken har en spole eller en kondensator. Värdet på detta motstånd bestäms av summan av spolens och anslutningstrådarnas aktiva motstånd. Vid vilken effektiv ström i kretsen kommer att vara den största och bestäms av Ohms lagformel I = U / R där Z nu ersätts av R.
Samtidigt kommer spänningarna som verkar på spolen UL = AzxL och på kondensatorn Uc = AzNSCC att vara lika stora och vara så stora som möjligt. Med lågt aktivt motstånd i kretsen kan dessa spänningar många gånger överstiga den totala spänningen U för kretsklämmorna. Detta intressanta fenomen kallas spänningsresonans inom elektroteknik.
I fig. 1 visar kurvorna för spänningar, strömmar och effekt vid resonansspänningar i kretsen.
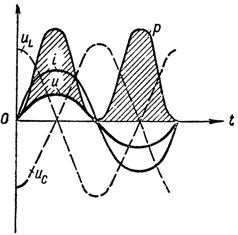
Graf över spänningsström och effekt vid spänningsresonans
Man bör komma ihåg att motstånden XL och C är variabler som beror på strömmens frekvens och det är värt att åtminstone ändra dess frekvens något, till exempel att öka den eftersom XL = ωL kommer att öka och XSC = = 1 / ωC kommer att minska och därmed kommer spänningsresonansen i kretsen omedelbart att störas, medan tillsammans med det aktiva motståndet kommer reaktansen att dyka upp i kretsen. Samma sak kommer att hända om du ändrar värdet på kretsens induktans eller kapacitans.
Med spänningsresonans kommer strömkällans kraft att användas endast för att övervinna kretsens aktiva motstånd, det vill säga att värma ledningarna.
Faktum är att i en krets med en enda induktiv spole uppstår energifluktuationer, d.v.s. periodisk överföring av energi från generatorn till magnetiskt fält spolar. I en krets med en kondensator händer samma sak, men på grund av energin i kondensatorns elektriska fält. I en krets med en kondensator och en induktor vid spänningsresonans (ХL = XС) passerar energin, när den väl har lagrats av kretsen, periodiskt från spolen till kondensatorn och vice versa, och endast den energiförbrukning som krävs för att övervinna det aktiva motståndet hos kretsen faller på andelen av strömkällan. Därför sker energiutbytet mellan kondensatorn och spolen nästan utan medverkan av generatorn.
Man behöver bara bryta en spänningsresonans efter värde, hur energin i spolens magnetfält blir ojämlik energin i kondensatorns elektriska fält, och i processen för energiutbyte mellan dessa fält kommer ett överskott av energi att visas, som med jämna mellanrum kommer att flöda ut från källan i kretsen, och sedan mata tillbaka den till den i kretsen.
Detta fenomen är väldigt likt det som händer i ett urverk. En klocks pendel skulle kunna svänga kontinuerligt utan hjälp av en fjäder (eller en vikt i en klockrullator) om det inte vore för friktionskrafterna som bromsar dess rörelse.
Fjädern, genom att överföra en del av sin energi till pendeln i rätt ögonblick, hjälper den att övervinna friktionskrafterna och på så sätt uppnå kontinuitet i svängningen.
På liknande sätt, i en elektrisk krets, när resonans uppstår i den, spenderar strömkällan sin energi endast för att övervinna kretsens aktiva motstånd, vilket hjälper den oscillerande processen i den.
Därmed kommer vi fram till att en växelströmskrets, bestående av en generator och en seriekopplad induktor och kondensator, under vissa förutsättningar XL = XС blir ett oscillerande system... Denna krets fick namnet en oscillerande krets.
Från ekvationen XL = XС är det möjligt att bestämma värdena för generatorns frekvens vid vilken fenomenet spänningsresonans inträffar:
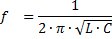
Betyder kapacitans och induktans för kretsen där spänningsresonans uppstår:
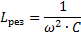
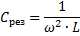
Således, genom att ändra någon av dessa tre kvantiteter (eres, L och C), är det möjligt att orsaka spänningsresonans i kretsen, det vill säga att förvandla kretsen till en oscillerande krets.
Ett exempel på en användbar tillämpning av spänningsresonans: Ingångskretsen för en mottagare justeras av en variabel kondensator (eller variometer) på ett sådant sätt att spänningsresonans uppstår i den. Detta uppnår en stor ökning av spolspänningen som krävs för normal mottagardrift jämfört med kretsspänningen som skapas av antennen.
Tillsammans med den användbara användningen av fenomenet spänningsresonans inom elektroteknik, finns det ofta fall där spänningsresonans är skadlig En stor ökning av spänningen i enskilda delar av kretsen (på spolen eller på kondensatorn) jämfört med spänningen av generatorn kan leda till skador på separata delar och mätanordningar.

