Vad är växelström och hur skiljer den sig från likström

Växelström, Däremot Likström, förändras ständigt både i storlek och riktning, och dessa förändringar inträffar periodiskt, det vill säga de upprepar sig med exakt lika intervall.

För att inducera en sådan ström i kretsen, använd växelströmskällor som skapar en växel-EMK, som periodiskt ändras i storlek och riktning. Sådana källor kallas växelströmsgeneratorer.

I fig. 1 visar ett anordningsdiagram (modell) av de enklaste generator. 

En rektangulär ram gjord av koppartråd, fixerad på axeln och roterad i fält med hjälp av en remdrift magnet… Ramens ändar är fastlödda i kopparringar som, roterande med ramen, glider på kontaktplattorna (borstarna).

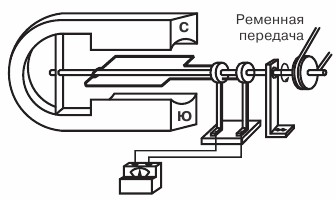
Figur 1. Diagram över den enklaste generatorn

Låt oss se till att en sådan enhet verkligen är en källa till variabel EMF.

Antag att en magnet skapar mellan dess poler enhetligt magnetfält, det vill säga en där tätheten av magnetiska fältlinjer i varje del av fältet är densamma.roterande korsar ramen magnetfältets kraftlinjer på var och en av dess sidor a och b EMF inducerad. 

Sidorna c och d på ramen fungerar inte, för när ramen roterar korsar de inte magnetfältets kraftlinjer och deltar därför inte i skapandet av EMF.

När som helst är den EMF som uppträder på sida a motsatt i riktning mot den EMF som förekommer på sidan b, men i ramen verkar båda EMF:erna enligt och adderar till den totala EMF, det vill säga inducerad av hela ramen.

Detta är lätt att kontrollera om vi använder högerregeln vi känner till för att bestämma EMF:s riktning.

För att göra detta, placera handflatan på höger hand så att den är vänd mot magnetens nordpol, och den böjda tummen sammanfaller med rörelseriktningen för den sida av ramen där vi vill bestämma EMF:s riktning. Då kommer riktningen för EMF i den att indikeras av handens utsträckta fingrar.

För vilken position som helst av ramen vi bestämmer riktningen för EMF i sidorna a och b, de summerar alltid och bildar en total EMF i ramen. Samtidigt, med varje rotation av ramen, ändras riktningen för den totala EMF i den till motsatt, eftersom var och en av arbetssidorna av ramen i ett varv passerar under olika poler av magneten.

Storleken på den EMF som induceras i ramen ändras också när hastigheten med vilken ramens sidor korsar magnetfältslinjerna ändras. I det ögonblick då ramen närmar sig sitt vertikala läge och passerar den, är hastigheten för att korsa kraftlinjerna på ramens sidor den högsta, och den största emk induceras i ramen.I dessa ögonblick, när ramen passerar sitt horisontella läge, verkar dess sidor glida längs magnetfältslinjerna utan att korsa dem, och ingen EMF induceras.

Därför, med enhetlig rotation av ramen, kommer en EMF att induceras i den, som periodiskt ändras både i storlek och riktning.

EMF som uppstår i ramen kan mätas av en enhet och användas för att skapa en ström i den externa kretsen.

Använder sig av fenomenet elektromagnetisk induktion, kan du få växel-EMK och därför växelström.

Växelström för industriella ändamål och för belysning produceras av kraftfulla generatorer som drivs av ång- eller vattenturbiner och förbränningsmotorer.

Grafisk representation av AC- och DC-strömmar

Den grafiska metoden gör det möjligt att visualisera processen att ändra en viss variabel beroende på tid.

Att plotta variabler som förändras över tiden börjar med att plotta två ömsesidigt vinkelräta linjer som kallas grafens axlar. Sedan, på den horisontella axeln, på en viss skala, plottas tidsintervall, och på den vertikala axeln, även på en viss skala, värdena för den kvantitet som ska plottas (EMF, spänning eller ström).

I fig. 2 grafiska likström och växelström ... I detta fall fördröjer vi strömvärdena och strömvärdena i en riktning, som vanligtvis kallas positiva, fördröjs vertikalt från skärningspunkten för axlarna O , och ner från denna punkt, den motsatta riktningen, som vanligtvis kallas negativ.

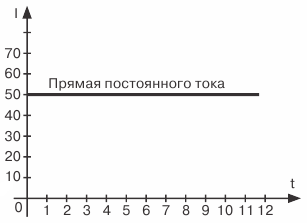
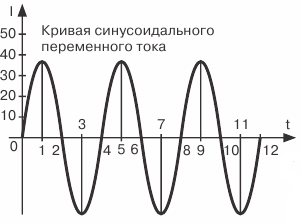Figur 2. Grafisk representation av DC och AC

Punkt O i sig fungerar både som ursprunget för nuvarande värden (vertikalt ner och upp) och tid (horisontellt höger).Denna punkt motsvarar med andra ord strömmens nollvärde och denna utgångspunkt från vilken vi avser att spåra hur strömmen kommer att förändras i framtiden.

Låt oss verifiera riktigheten av det som plottas i fig. 2 och en 50 mA DC-strömplot.

Eftersom denna ström är konstant, det vill säga den ändrar inte dess storlek och riktning över tiden, kommer samma strömvärden att motsvara olika tidpunkter, det vill säga 50 mA. Därför, vid tidpunkten lika med noll, det vill säga i det första ögonblicket av vår observation av strömmen, kommer den att vara lika med 50 mA. Genom att rita ett segment lika med det aktuella värdet på 50 mA på den vertikala axeln uppåt får vi den första punkten i vår graf.

Vi måste göra samma sak för nästa ögonblick i tiden som motsvarar punkt 1 på tidsaxeln, det vill säga skjuta upp från denna punkt vertikalt uppåt ett segment som också är lika med 50 mA. Slutet av segmentet kommer att definiera den andra punkten i grafen för oss.

Efter att ha gjort en liknande konstruktion för flera efterföljande tidpunkter får vi en serie punkter, vars anslutning kommer att ge en rät linje, vilket är en grafisk representation av ett konstant strömvärde på 50 mA.

Plotta en variabel EMF

Låt oss gå vidare till att studera variabel graf för EMF... I fig. I figur 3 visas en ram som roterar i ett magnetfält överst, och en grafisk representation av den resulterande variabeln EMF ges nedan.

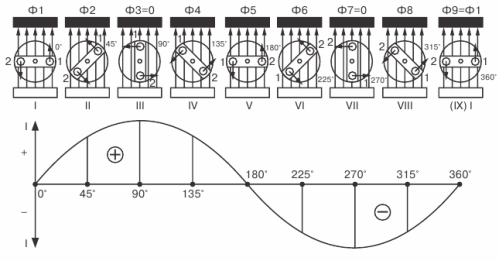Figur 3. Plotta variabeln EMF

Vi börjar rotera ramen jämnt medurs och följer EMF-förändringarna i den, och tar ramens horisontella position som det första ögonblicket.

Vid detta första ögonblick kommer EMF att vara noll eftersom ramens sidor inte korsar magnetfältslinjerna.På grafen representeras detta nollvärde av EMF som motsvarar ögonblicket t = 0 av punkt 1.

Med ytterligare rotation av ramen kommer EMF att börja dyka upp i den och kommer att öka tills ramen når sitt vertikala läge. På grafen kommer denna ökning av EMF att representeras av en jämn stigande kurva som når sin topp (punkt 2).

När ramen närmar sig det horisontella läget kommer EMF i den att minska och sjunka till noll. På grafen kommer detta att avbildas som en fallande jämn kurva.

Under den tid som motsvarar ett halvt varv av ramen kunde därför EMF i den öka från noll till maxvärdet och minska till noll igen (punkt 3).

Med ytterligare rotation av ramen kommer EMF att dyka upp igen i den och gradvis öka i storlek, men dess riktning kommer redan att ändras till motsatt, vilket kan ses genom att tillämpa högerregeln.

Grafen tar hänsyn till förändringen i EMF:s riktning, så att kurvan som representerar EMF korsar tidsaxeln och nu ligger under den axeln. EMF ökar igen tills ramen intar ett vertikalt läge.

Sedan kommer EMF att börja minska och dess värde blir lika med noll när ramen återgår till sin ursprungliga position efter att ha fullbordat ett helt varv. På grafen kommer detta att uttryckas genom att EMF-kurvan, som når sin topp i motsatt riktning (punkt 4), då möter tidsaxeln (punkt 5)

Detta avslutar en cykel av att ändra EMF, men om du fortsätter rotationen av ramen, börjar den andra cykeln omedelbart, exakt upprepa den första, som i sin tur kommer att följas av den tredje, sedan den fjärde, och så vidare tills vi slutar rotationsramen.

Sålunda, för varje rotation av ramen, fullbordar EMF som förekommer i den en fullständig cykel av dess förändring.

Om ramen är stängd för någon extern krets, kommer en växelström att flyta genom kretsen, vars graf kommer att se ut som EMF-grafen.

Den resulterande vågformen kallas en sinusvåg, och strömmen, EMF eller spänningen som varierar enligt denna lag kallas sinusformad.

Själva kurvan kallas en sinusform eftersom den är en grafisk representation av en variabel trigonometrisk storhet som kallas sinus.

Den sinusformade karaktären av strömändringen är den vanligaste inom elektroteknik, därför, på tal om växelström, betyder de i de flesta fall sinusformad ström.

För att jämföra olika växelströmmar (EMF och spänningar) finns det värden som kännetecknar en viss ström. Dessa kallas AC-parametrar.

Period, Amplitud och Frekvens — AC-parametrar

Växelström kännetecknas av två parametrar — månadscykel och amplitud, med vetskap om vilken vi kan uppskatta vilken typ av växelström det är och bygga en graf över strömmen.

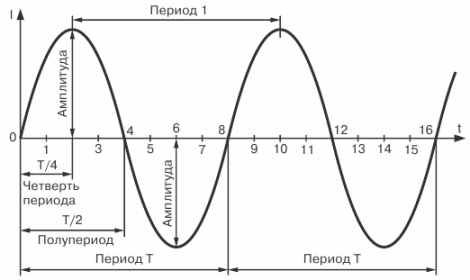
Figur 4. Sinusformad strömkurva

Den tidsperiod under vilken en fullständig cykel av nuvarande förändring inträffar kallas en period. Perioden betecknas med bokstaven T och mäts i sekunder.

Den tidsperiod under vilken halva en hel cykel av strömförändringar inträffar kallas en halvcykel.Därför består perioden för strömförändring (EMF eller spänning) av två halva perioder. Det är ganska uppenbart att alla perioder av samma växelström är lika med varandra.

Som framgår av grafen, under en period av dess förändring, når strömmen två gånger sitt maximala värde.

Det maximala värdet för en växelström (EMF eller spänning) kallas dess amplitud eller toppströmvärde.

Im, Em och Um är vanliga beteckningar för ström-, EMF- och spänningsamplituder.

Först och främst var vi uppmärksamma toppström, men som kan ses från grafen finns det otaliga mellanvärden som är mindre än amplituden.

Värdet på växelström (EMF, spänning) som motsvarar varje valt ögonblick kallas dess momentana värde.

i, e och u är allmänt accepterade beteckningar för de momentana värdena för ström, emk och spänning.

Strömmens momentana värde, liksom dess toppvärde, är lätta att bestämma med hjälp av grafen. För att göra detta, från vilken punkt som helst på den horisontella axeln som motsvarar den tidpunkt vi är intresserade av, dra en vertikal linje till skärningspunkten med den aktuella kurvan; det resulterande segmentet av den vertikala linjen kommer att bestämma värdet på strömmen vid en given tidpunkt, det vill säga dess momentana värde.

Uppenbarligen kommer det momentana värdet av strömmen efter tid T / 2 från startpunkten för grafen att vara noll, och efter tid T / 4 dess amplitudvärde. Strömmen når också sitt toppvärde; men redan i motsatt riktning, efter en tid lika med 3/4 T.

Så grafen visar hur strömmen i kretsen förändras över tiden och att endast ett särskilt värde av både storleken och riktningen av strömmen motsvarar varje ögonblick av tid. I detta fall kommer värdet på strömmen vid en given tidpunkt vid en punkt i kretsen att vara exakt detsamma vid vilken annan punkt som helst i den kretsen.

Det kallas antalet fullständiga perioder som uppfylls av strömmen i 1 sekund av AC-frekvensen och betecknas med den latinska bokstaven f.

För att bestämma frekvensen för en växelström, det vill säga för att ta reda på hur många perioder av dess förändring strömmen gjort på 1 sekund, är det nödvändigt att dividera 1 sekund med tiden för en period f = 1 / T. Att känna till frekvensen av växelströmmen kan du bestämma perioden: T = 1 / f

AC frekvens den mäts i en enhet som kallas hertz.

Om vi ​​har en växelström vars frekvens är lika med 1 hertz, kommer perioden för en sådan ström att vara lika med 1 sekund. Omvänt, om ändringsperioden för strömmen är 1 sekund, är frekvensen för en sådan ström 1 hertz.

Så vi har definierat växelströmsparametrar – period, amplitud och frekvens – som gör att du kan skilja mellan olika växelströmsströmmar, EMF:er och spänningar, och plotta deras grafer när det behövs.

Vid bestämning av olika kretsars resistans mot växelström, använd ett annat hjälpvärde som kännetecknar växelström, s.k. vinkel- eller vinkelfrekvens.

Cirkulär frekvens betecknad relaterad till frekvens f med förhållandet 2 pif

Låt oss förklara detta beroende. När vi ritade den variabla EMF-grafen såg vi att en fullständig rotation av ramen resulterar i en komplett cykel av EMF-förändring. Med andra ord, för ramen att göra ett varv, det vill säga att rotera 360°, tar det en tid lika med en period, det vill säga T sekunder. Sedan, på 1 sekund, gör ramen ett varv på 360 °/T. Därför är 360 ° / T vinkeln genom vilken ramen roterar på 1 sekund, och uttrycker ramens rotationshastighet, vilket vanligtvis kallas vinkel- eller cirkulär hastighet.

Men eftersom perioden T är relaterad till frekvensen f med förhållandet f = 1 / T, kan cirkulärhastigheten också uttryckas som en frekvens och kommer att vara lika med 360 ° f.

Så vi drog slutsatsen att 360 ° f. Men för att underlätta användningen av den cirkulära frekvensen för alla beräkningar, ersätts 360°-vinkeln som motsvarar ett varv med ett radiellt uttryck lika med 2pi radianer, där pi = 3,14. Så vi får äntligen 2pif. Därför, för att bestämma vinkelfrekvensen för växelström (EMF eller spänning), måste du multiplicera frekvensen i hertz med ett konstant tal 6,28.