Logiska enheter

Logisk algebra eller boolesk algebra används för att beskriva funktionslagarna för digitala kretsar. Logikens algebra bygger på konceptet om en "händelse" som kan hända eller inte. En händelse som har inträffat anses sann och en logisk nivå «1» uttrycks, en händelse som inte har inträffat anses vara falsk och en logisk nivå «0» uttrycks.

Händelsen påverkas av variabler och de påverkar enligt en viss lag. Denna lag kallas en logisk funktion, variablerna är argument... Che. den logiska funktionen är funktionen y = f (x1, x2, … xn), som tar värdena «0» eller «1». Variablerna x1, x2, … xn har också värdena «0» eller «1».

Logikens algebra — en gren av matematisk logik som studerar strukturen hos komplexa logiska påståenden och sätt att fastställa deras sanning med algebraiska metoder. I formlerna för logisk algebra är variablerna logiska eller binära, det vill säga de tar bara två värden - falskt och sant, som betecknas med 0 respektive 1. Varje datorprogram innehåller logiska operationer.

Enheter som utformats för att bilda funktioner i den logiska algebra kallas logiska enheter... En logisk enhet har valfritt antal ingångar och bara en utgång (Fig. 1).

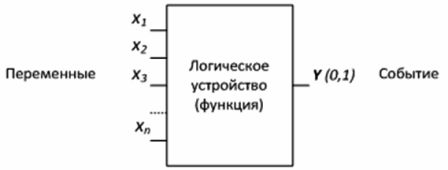
Figur 1 — Logisk enhet

Till exempel inkluderar ett elektroniskt kombinationslås en logisk anordning för vilken händelse (y) är låsets öppning. För att händelsen (y = 1) ska inträffa, dvs. låset har öppnats är det nödvändigt att definiera variablerna — tio knappar på det numeriska tangentbordet. Vissa knappar måste tryckas in, dvs. ta värdet «1» och tryck samtidigt i en viss sekvens — en logisk funktion.

Det är bekvämt att representera vilken logisk funktion som helst i form av en tillståndstabell (sanningstabell), där möjliga kombinationer av variabler (argument) och motsvarande värde för funktionen registreras.

Logiska enheter är byggda på logiska grindar som utför en specifik funktion. De grundläggande logiska funktionerna är logisk addition, logisk multiplikation och logisk negation.

1) ELLER (ELLER) — logisk addition eller division (från engelsk disjunction — interruption) — en logisk enhet visas vid utgången av detta element när en enhet förekommer vid åtminstone en av ingångarna. Utgången blir logisk noll endast när det finns en logisk nollsignal på alla ingångar.

Denna operation kan åstadkommas med hjälp av en kontaktkrets med två parallellkopplade kontakter. «1» vid utgången av en sådan krets visas om minst en av kontakterna är sluten.

2) OCH (AND) — logisk multiplikation eller anslutning (från den engelska unionen — anslutning, & — et-tecken) — vid utgången av detta element visas signalen från en logisk enhet endast när en logisk enhet finns vid alla ingångar.Om minst en ingång är noll, kommer utsignalen också att vara noll.

Denna operation kan utföras av en kontaktkrets som består av kontakter kopplade i serie.

3) NOT – logisk negation eller inversion indikerad med ett bindestreck ovanför en variabel – operationen utförs på en variabel x och värdet på y är motsatsen till den variabeln.

Operationen kan INTE utföras med en normalt sluten kontakt på det elektromagnetiska reläet: det finns ingen spänning på reläspolen (x = 0) — kontakten är också sluten på utgången «1» (y = 1). I närvaro av spänning på reläspolen (x = 1) är kontakten också öppen på «0»-utgången (y = 0).

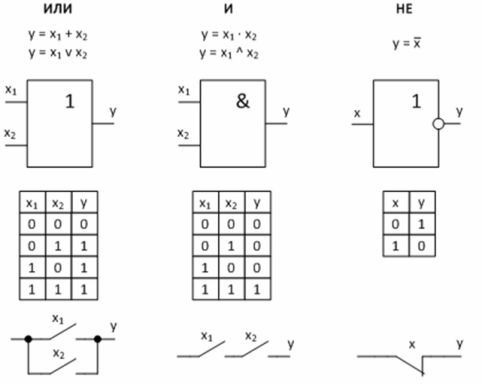
Figur 2 — Grundläggande logiska funktioner och deras implementering

Logiska enheter använder olika logiska grindar. Särskilt viktiga är två universella logiska operationer, som var och en är kapabel att oberoende bilda vilken logisk funktion som helst.

4) NAND — Schäfer-funktion.

5) ELLER INTE — Hålslagsfunktion.

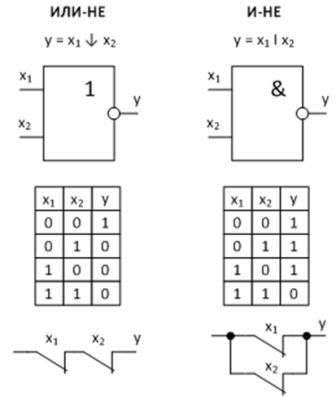
Figur 3 — Universella logiska funktioner och deras implementering

Exempel: Säkerhetslarmkrets baserad på logiska element. Generator G genererar en sirensignal som matar den till förstärkarsteget genom det logiska elementet «OCH» i mikrokretsen DD2. När skyddsomkopplarna S1 — S4 är slutna, verkar nivån «0» på ingångarna till elementet DD1 — nivån «0» är på den nedre ingången av elementet «I» DD2, vilket betyder att transistorns gate VT är också «0».

I fallet med att öppna minst en av omkopplarna, till exempel S1, kommer ingången till elementet DD1 genom motståndet R1 att få en spänning på nivån «1», vilket kommer att orsaka utseendet på «1» vid den andra ingången på elementet «OCH» DD1.Detta kommer att tillåta signalen från generatorn G att passera till porten på transistorn vars belastning är högtalaren.

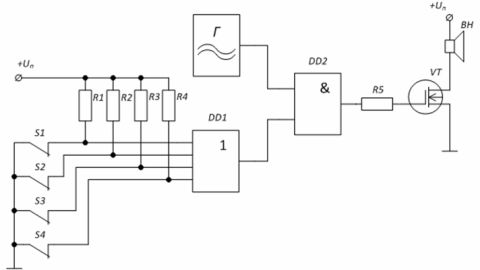
Figur 4 — Larmskyddsschema

Komplexa digitala kretsar byggs genom att upprepa grundläggande logiska kretsar om och om igen. Verktyget för en sådan konstruktion är boolesk algebra, som i termer av digital teknik kallas logisk algebra. Till skillnad från en variabel i vanlig algebra har en boolesk variabel bara två värden, som kallas boolesk noll och boolesk etta.

Logisk nolla och logisk etta betecknas med 0 och 1. I logisk algebra är 0 och 1 inte tal, utan logiska variabler. I logisk algebra finns det tre grundläggande operationer mellan logiska variabler: logisk multiplikation (konjunktion), logisk addition (disjunktion) och logisk negation (inversion).

Elektroniska kretsar som utför samma logiska funktion, men sammansatta med olika element, skiljer sig åt i strömförbrukning, matningsspänning, värden på höga och låga utspänningsnivåer, signalutbredningsfördröjningstid och belastningskapacitet.

Se även om detta ämne: AND, OR, NOT, AND-NOT, OR-NOT logiska grindar och deras sanningstabeller