Elektrokapillära fenomen

Om elektrolytens yta är laddad, beror ytspänningen på dess yta inte bara på den kemiska sammansättningen av de närliggande faserna, utan också på deras elektriska egenskaper. Dessa egenskaper är ytladdningstätheten och potentialskillnaden vid gränsytan.

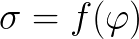
Ytspänningens beroende (e) av potentialskillnaden för detta fenomen beskrivs av en elektrokapillär kurva. Och själva ytfenomenen där detta beroende observeras kallas elektrokapillära fenomen.

Låt elektrodpotentialen ändras på något sätt vid gränssnittet mellan elektrod och elektrolyt. I det här fallet finns det joner på metallytan som bildar en ytladdning och orsakar närvaron av ett elektriskt dubbelskikt, även om det inte finns någon extern EMF här alls.

Liknande laddade joner stöter bort varandra över ytan av gränsytan och kompenserar på så sätt för vätskemolekylernas kontraktila krafter. Som ett resultat blir ytspänningen lägre än i frånvaro av en överskottspotential på elektroden.

Om en laddning med motsatt tecken appliceras på elektroden, kommer ytspänningen att öka eftersom krafterna för ömsesidig repulsion av joner kommer att minska.

Vid absolut kompensation av attraktionskrafterna med de elektrostatiska krafterna från de repulsiva jonerna når ytspänningen ett maximum. Om vi ​​fortsätter att tillföra laddningen kommer ytspänningen att minska när ny ytladdning kommer att uppstå och växa.

I vissa fall är betydelsen av elektrokapillära fenomen mycket stor. De gör det möjligt att förändra ytspänningen hos vätskor och fasta ämnen, samt att påverka kolloid-kemiska processer som vidhäftning, vätning och dispersion.

Låt oss åter vända vår uppmärksamhet till den kvalitativa sidan av detta beroende. Termodynamiskt definieras ytspänning som arbetet med den isotermiska processen att bilda en enhetsyta.

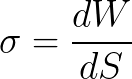
När det finns elektriska laddningar med samma namn på en yta kommer de att stöta bort varandra elektrostatiskt. Krafterna av elektrostatisk repulsion kommer att riktas tangentiellt mot ytan, och försöka öka dess yta ändå. Som ett resultat kommer arbetet för att sträcka den laddade ytan att vara mindre än det arbete som skulle krävas för att sträcka en liknande men elektriskt neutral yta.

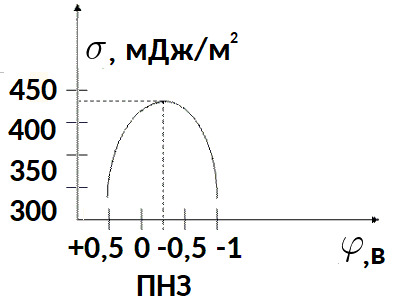
Som ett exempel, låt oss ta den elektrokapillära kurvan för kvicksilver i vattenlösningar av elektrolyter vid rumstemperatur.

Vid punkten för maximal ytspänning är laddningen noll. Kvicksilverytan är elektriskt neutral under dessa förhållanden.Således är den potential vid vilken elektrodens ytspänning är maximal nollladdningspotentialen (ZCP).

Storleken på potentialen för nollladdning är relaterad till den flytande elektrolytens natur och lösningens kemiska sammansättning. Den vänstra sidan av den elektrokapillära kurvan, där ytpotentialen är mindre än potentialen för nollladdning, kallas den anodiska grenen. Den högra sidan är katodgrenen.

Det bör noteras att mycket små förändringar i potential (i storleksordningen 0,1 V) kan ge märkbara förändringar i ytspänningen (i storleksordningen 10 mJ per kvadratmeter).

Ytspänningens beroende av potentialen beskrivs av Lippmann-ekvationen:

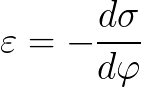
Elektrokapillära fenomen finner praktisk tillämpning vid applicering av olika beläggningar på metaller — de gör det möjligt att reglera vätning av fasta metaller med vätskor. Lippmann-ekvationen tillåter beräkning av ytladdningen och kapacitansen för det elektriska dubbelskiktet.

Med hjälp av elektrokapillära fenomen bestäms ytaktiviteten hos ytaktiva ämnen, eftersom deras joner har en specifik adsorption. I smälta metaller (zink, aluminium, kadmium, gallium) bestäms deras adsorptionsförmåga.

Den elektrokapillära teorin förklarar maxima i polarografi. Beroendet av elektrodens vätbarhet, hårdhet och friktionskoefficient på dess potential hänvisar också till elektrokapillära fenomen.